Best practices for machine-learned force fields
Using the machine-learning-force-fields method, VASP can construct force fields based on ab-initio simulations. When constructing, testing, re-learning, and applying a force field, many aspects must be carefully considered. Some best practices are listed here, but note that the list is not exhaustive and the method has not yet been applied to a large number of systems. We, therefore, recommend the usual rigorous monitoring that is necessary for all research projects. The basic steps required for machine learning force field (MLFF) training can be found on the Basics page on machine learning force field calculations.
Training
Best practice training modes
To start a training run, set ML_MODE = TRAIN. Depending on the existence of a valid ML_AB in the folder where VASP is executed, one of the two modes is automatically selected:
- No ML_AB file: the training algorithm will start from zero.
- ML_AB file is present: Training will continue based on an existing structure database. In this mode of operation, a force field is generated from the existing database (ML_AB file) and then a MD run is continued from the specified POSCAR file. This mode is used to select additional structures from the phase space of the material. But it can also be used to examine surfaces by first training the bulk material, then adding a molecule to the surface in the POSCAR file and continuing the training.
If there are several atoms of the same species which should be treated differently by the machine-learning algorithm it is important to give different names to them in the POSCAR file. For example if there are oxygen atoms in a bulk material and in a molecule at the surface it is advisable to make two groups of oxygen atoms in the POSCAR and call one group O1 and and the second O2.
| Warning: It is not possible to give the same name to different groups of atoms in the POSCAR file and the names are restricted to two characters. |
The training mode requires VASP to perform ab-initio calculations, so the first step is to set up the electronic minimization scheme.
| Warning: It is very important to not change the ab-initio settings in the INCAR file between training from scratch and continuing training. Likewise, the POTCAR file is not allowed to be changed when resuming training. |
Ab-initio calculation setup
In general, everything that applies to VASP DFT calculations also applies here. The guidelines for electronic minimization can be used to set up the ab-initio part for on-the-fly training. Additionally, we strongly advise following these guidelines for ab-initio computation during on-the-fly learning:
- Do not set MAXMIX>0 when using force fields for machine learning. During machine learning, first-principles calculations are often bypassed for hundreds or even thousands of ion steps, and ions can move significantly between first-principles calculations. In these cases, the use of MAXMIX very often results in non-converged electronic structures or errors during the self-consistency cycle.
- It is generally possible to train force fields on a smaller unit cell and then apply them to a larger system. Be sure to choose a large enough structure so that the phonons or collective oscillations "fit" into the supercell.
- It is important to learn the exact forces. To do this, the electronic minimization has to be checked for convergence. These checks may include, for example, the number of k-points in the KPOINTS file, the plane wave limit (ENCUT), the electronic minimization algorithm, etc.
- Turn off symmetry as for standard molecular dynamics runs (ISYM=0).
- For simulations without a fixed grid (NpT), the cutoff for plane waves ENCUT must be set at least 30 percent higher than for fixed volume calculations. Also, it is good to restart frequently (ML_MODE=TRAIN with existing ML_AB file in working directory) to reinitialize the PAW basis of KS orbitals and avoid Pulay stress.
Molecular dynamics setup
After the forces are obtained from electronic minimization by the Hellmann-Feynman Theorem, VASP must propagate the ions to obtain a new configuration in phase space. For the molecular dynamics part, familiarity with setting up molecular dynamics runs is beneficial. In addition, we recommend the following settings in the molecular dynamics part:
- Decrease the integration step (POTIM) if the system contains light elements, or increase the light element mass (POMASS) in the INCAR or the POTCAR file. As a rule of thumb, the time step should not exceed 0.7 fs and 1.5 fs for hydrogen and oxygen-containing compounds, respectively. However, a time step of 3 fs may work well for heavy elements (Si).
- If possible, heat the system gradually using the temperature ramp (set TEEND higher than TEBEG). Start with a low temperature (not zero) and increase it to a temperature about 30% above the desired application temperature. This will help "on-the-fly" training to explore a larger portion of the phase space and will result in more stable force fields.
- If possible, prefer molecular dynamics training runs in the NpT ensemble (ISIF=3). The additional cell fluctuations improve the robustness of the resulting force field. However, for fluids, only volume changes of the supercell are allowed, otherwise, the cell may "collapse", i.e., it tilts extremely so that the system becomes a layer of atoms. This can be achieved with ICONST, here and here. For an example input for constraining the cell shape, see the ICONST page or the end of this page page. The NVT ensemble (ISIF=2) is also acceptable for training, but use the Langevin thermostat as it is very good for phase space sampling (ergodicity) due to its stochastic nature.
- One should always try to explore as much of the phase space of the material as possible. Therefore, one should always avoid training in the NVE ensemble.
General settings for on the fly training
The ML_MODE=TRAIN sets already widely used default values for on-the-fly training in machine learning. Nevertheless, we would like to provide the following guidelines for setting individual machine-learning parameters:
- If the system contains different components, first train them separately. For example, if the system consists of a crystal surface and a molecule that binds to that surface. Train the main crystal first, then the surface, possibly the isolated molecule, and finally the entire system (if you do not need to describe the isolated molecule, you can skip training for the molecule). In this way, a considerable number of ab-initio calculations can be avoided in the most computationally intensive combined system.
- If there are not enough reference configurations taken during training (seen in ML_ABN), adjusting the default value of ML_EPS_LOW should be used to sparsify the local reference configurations used from the ML_AB. This can improve the performance of the trained force field. However, it may also reduce the accuracy.
| Mind: Hyperparameter optimization should always be started from default values |
| Mind: For fluids, reducing to ML_LMAX2=2 and ML_RCUT2=4 can lead to better fitting results. |
Accuracy
The achievable accuracy of the force fields depends on many factors, e.g. species, temperature, pressure, electronic convergence, machine learning method, etc. In our implementation of kernel ridge regression, the accuracy of the force fields increases as the number of local reference configurations increases. This increase is not linear and at the same time, the computational cost increases linearly. When generating machine-learning force fields there is always a tradeoff between accuracy and efficiency.
Here are some empirical guidelines:
- For a given structure, the error increases with increasing temperature and pressure. Therefore, the force field should not be trained under conditions too far from the target condition. For example, for a production run at 300 K, it is good to learn above this temperature (450-500 K) to capture more structures that might occur in the production run, but it is not beneficial to learn the same phase at, say, 1000 K, as this is likely to reduce the accuracy of the force field.
- Liquids typically require many more training structures and local reference configurations to achieve similar accuracy to solids. To achieve errors of about 30 meV/angstrom, liquids often require 2000-4000 local reference configurations, while 500-1000 reference configurations might be sufficient for simple periodic volume systems.
- Typically, the fitting errors should be less than 1 meV/atom for the energies and 30-100 meV/angstrom for the forces at temperatures between 300-1000 K. Errors slightly above these values may be acceptable, but these calculations should be thoroughly checked for accuracy.
Accurate force fields
The default parameters that control learning and sampling are chosen to provide a good tradeoff between accuracy and efficiency. In particular, the default setting for ML_EPS_LOW tends to remove local reference configurations during the sparsification step, limiting accuracy. However, further decreasing ML_EPS_LOW to values below 1.0E-11 does not improve accuracy, since the condition number of the regularized normal equation solved in Bayesian regression is approximately proportional to the square of the condition number of the Gram matrix considered during sparsification (see here). Thus, if the Gram matrix has a condition number of 1E9, then the normal equation has a condition number of 1E18, which means that a loss of significance occurs when the normal equation is solved.
To obtain highly accurate force fields that retain more local reference configurations, one must use the following two-step procedure:
First, one performs a full on-the-fly learning:
ML_IALGO_LINREG=1; ML_SION1=0.3; ML_MRB2=12
This can consist of many different training steps that include all the desired structures. Increasing ML_MRB1 from 8 to 12 and decreasing ML_SION1 from 0.5 to 0.3 improves the condition number of the Gram matrix by about a factor of 10 and allows the sparsification step to retain more local reference configurations (typically by about a factor of 2). Of course, this slows down the force field calculations somewhat.
If full retraining is not possible, you can also try to increase only the number of local reference calculations, as described above, by using ML_MODE=SELECT and choosing a value for ML_CTIFOR that gives a satisfactory number of local reference configurations.
Second, readjust the force field using ML_MODE=REFIT.
Using SVD instead of solving the regularized normal equation avoids squaring the problem, and therefore the condition number of the design matrix rather than its square is important. In our experience, SVD refinement with the default value ML_SION1=0.5 always improves the accuracy of the force field.
Tuning on-the-fly parameters
In case too many or too few training structures and local reference configurations are selected some on-the-fly parameters can be tuned (for an overview of the learning and threshold algorithms we may refer here):
- ML_CTIFOR: Defines the learning threshold for the Bayesian error of the forces for each atom. In a continuation run, it can be set to the last value of ML_CTIFOR of the previous run. This way unnecessary sampling at the beginning of the calculation can be skipped. However, when going from one structure to the other, this tag should be very carefully set. ML_CTIFOR is species and system dependent. Low symmetry structures, for example, liquids, have usually a much higher error than high symmetry solids for the same compound. If a liquid is learned first and the last ML_CTIFOR from the liquid is used for the corresponding solid, this ML_CTIFOR is way too large for the solid and all predicted errors will be below the threshold. Hence no learning will be done on the solid. In this case, it is better to start with the default value for ML_CTIFOR. Typical attainable values for ML_CTIFOR are 0.02 around 300-500 K, and 0.06 around 1000-2000 K, so temperature but also system dependent.
- ML_CX: It is involved in the calculation of the threshold, ML_CTIFOR = (average of the stored Bayesian errors in the history) *(1.0 + ML_CX). This tag affects the frequency of selection of training structures and local reference configurations. Positive values of ML_CX result in a less frequent sampling (and hence less ab-initio calculations) and negative values result in the opposite. Typical values of ML_CX are between -0.3 and 0. For training runs using heating, the default usually results in very well-balanced machine-learned force fields. When the training is performed at a fixed temperature, it is often desirable to decrease to ML_CX=-0.1, to increase the number of first principle calculations, and thus the size of the training set (the default can result in too few training data).
- ML_MHIS: Sets the number of previous Bayesian errors (from learning steps for the default of ML_ICRITERIA) that are used for the update of ML_CTIFOR. If, after the initial phase, strong variations of the Bayesian errors between updates of the threshold appear and the threshold also changes strongly after each update, the default of 10 for this tag can be lowered.
- ML_SCLC_CTIFOR: Scales ML_CTIFOR only in the selection of local reference configurations. In contrast, to ML_CX this tag does not affect the frequency of sampling (ab-initio calculations). Smaller values mean more local reference configurations are selected; large values mean fewer local reference configurations are selected.
- ML_EPS_LOW: Controls the sparsification of the number of local reference configurations after they were selected by the Bayesian error estimation. Increasing ML_EPS_LOW increases the number of local reference configurations that are removed and by decreasing the opposite happens. This tag will also not affect the learning frequency since the sparsification is only done after the local reference configurations were selected for a new structure. We do not recommend increasing the threshold to values larger than 1E-7. Below that value this tag works well to control the number of local reference configurations, however, for multi-component systems, the sparsification algorithm tends to lead to strong imbalances in the number of local reference configurations for different species.
- ML_LBASIS_DISCARD: Controls, whether the calculation continues or stops after the maximum number of local reference configurations ML_MB for any species is reached. Previously the default behavior was ML_LBASIS_DISCARD=.FALSE.: the calculation stops and requests an increase of ML_MB if the number of local reference configurations for any species reaches ML_MB. In multi-component systems, the sparse representation for one species exceeds ML_MB very quickly, while the other species are not sufficiently well described by the yet determined local reference configurations and are still far below the limit ML_MB. The present default is hence ML_LBASIS_DISCARD=.TRUE.: In this case, the code disposes of local reference configurations whenever the threshold is reached. It does this species dependent.
Monitoring on-the-fly learning
The monitoring of your learning can be divided into two parts:
- Molecular dynamics/ensemble-related quantities:
- Monitor your structure visually. This means looking at the CONTCAR or XDATCAR files with structure/trajectory viewers. Many times when something goes wrong it can be immediately traced back to unwanted or unphysical deformations.
- Volume and lattice parameters in the OUTCAR, XDATCAR and CONTCAR files. It is important to confirm that the average volume stays in the desired region. A strong change of the average volume over time in constant temperature and pressure runs indicates phase transitions or non-properly equilibrated systems. Particularly troublesome is a strong shearing during a single VASP run: since VASP keeps the plane wave basis set fixed and originally uses a spherical cutoff sphere, the cutoff sphere effectively becomes an ellipsoid. That is, the effective cutoff becomes small in some reciprocal lattice directions. Lattice vector changes of more than 10 % during a single run must be avoided. The corresponding data files ( ML_AB) are not suitable to continue the training (perform your calculations in small "junks").
- Temperature and pressure in the OUTCAR and OSZICAR files. Strong deviations of temperature and pressure to the desired ones at the beginning of the calculation indicate non-properly equilibrated starting positions. If the desired charasteristics undergo strong oscillations optionally block averages can be used to monitor them (for more on block averages please see below under "Application").
- Pair-correlation functions (PCDAT).
- Machine learning specific quantities in the ML_LOGFILE file:
- Estimation of required memory per core. It is written at the beginning of the ML_LOGFILE before allocations are done (see here). It is important that if the required memory exceeds the physically available memory the calculation won't necessarily immediately crash at the allocation of static arrays, since many systems use lazy allocations. The calculation could run for a long time before crashing with insufficient memory. Hence the memory estimation should always be checked after startup.
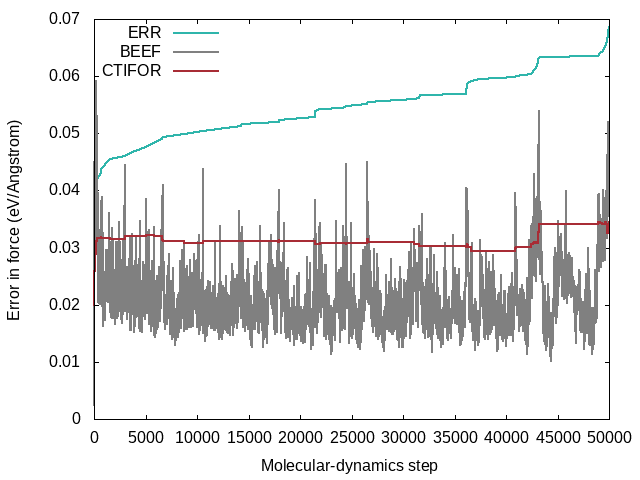
STATUS: Shows what happened at each molecular-dynamics steps. The force field is updated when the status is "learning/critical". Monitor this variable frequently from the beginning on (grep "STATUS" ML_LOGFILE.1|grep -E 'learning|critical'|grep -v "#"). If the calculation still updates the force field at every step after 50 iterations it is a sign that there is something seriously wrong with the calculation. The same is true if the calculation stops learning after a few steps and only force-field steps are carried out from then on. In both cases, no useful force field will come out. In ideal learning, the frequency of the update of the force field is high at the beginning and continuously decreases until the algorithm learns only sporadically. Note that due to the approximate error prediction of the Bayesian error, the learning frequency will never drop to zero. If the learning frequency increases suddenly in the late stages of a molecular dynamics run, it is usually a sign that a new region of phase space is explored, which is currently unknown to the force field. But this sudden increase in learning steps towards the end of training could also indicate unwanted deformations of the system that should be looked into carefully.LCONF: Number of local configurations at each learning step.ERR: Root mean square error of predicted energy, forces, and stress () concerning ab-initio data for all training structures up to the current molecular-dynamics step . Here goes over all training structures for the energies, element-wise over each training structure, times the number of atoms per structure times three Cartesian directions for the forces, and element-wise for each training structure times nine tensor components for the stress tensor.BEEF: Estimated Bayesian error of energy, forces, and stress (columns 3-5). The current threshold for the maximum Bayesian error of forces ML_CTIFOR on column 6.THRUPD: Update of ML_CTIFOR.THRHIST: History of Bayesian errors used for ML_CTIFOR.
A typical evolution of the real errors (column 4 of ERR), Bayesian errors (column 4 of BEEF), and threshold (column 6 of BEEF) for the forces looks like the following:
The following commands were used to extract the errors from the ML_LOGFILE:
grep ERR ML_LOGFILE|grep -v "#"|awk '{print $2, $4}' > ERR.dat
grep BEEF ML_LOGFILE|grep -v "#"|awk '{print $2, $4}' > BEEF.dat
grep BEEF ML_LOGFILE|grep -v "#"|awk '{print $2, $6}' > CTIFOR.dat
The following gnuplot script was used to plot the errors:
set key left top
set xlabel "Molecular-dynamics step"
set ylabel "Error in force (eV/Angstrom)"
set terminal png
set output 'ERR_BEEF_CTIFOR_vs_MD_step.png'
plot "ERR.dat" using 1:2 with lines lw 2 lt rgb "#2fb5ab" title "ERR", \
"BEEF.dat" using 1:2 with lines lw 2 lt rgb "#808080" title "BEEF", \
"CTIFOR.dat" using 1:2 with lines lw 2 lt rgb "#a82c35" title "CTIFOR"
- From the plot one can see that the Bayesian errors are always smaller than the real errors. Bayesian inference catches errors in the data well but still retains an error in the probability model.
- The plot was extracted from a heating run of liquid water. This can be nicely seen from the steadily increasing real error
ERRover the whole calculation. In a constant temperature run the error would usually plateau after some time. - The steps in the real error correspond to the molecular-dynamics steps where the force field is updated ('learning' or 'critical' for the
STATUS). This would be also evident from the change in the number of local reference configurations (grep "LCONF" ML_LOGFILE) at the same molecular-dynamics steps. - The following things can cause an increase in errors:
- Using a temperature ramp always results in steadily increasing errors.
- A sudden increase in errors (especially after being stable for some time) usually indicates deformations of the cell. Usually one wants to avoid these deformations and only train the "collective vibrations" of a given phase at different temperatures. Common causes of these deformations are too large temperatures leading to phase transitions or neglect of constraints (ICONST file) for liquids.
- The evidence approximation is over-fitting and the regularization cannot handle the over-fitting. This is a rare case, but if it happens one should start to reduce the fitting data by increasing ML_EPS_LOW.
Testing
Generating a representative test set
To assess the predictive power of your MLFF, start by generating a test set reflecting the conditions your force field will encounter. A good way to get test structures is to conduct a molecular dynamics (MD) run using the MLFF and then extract a chosen number of structures equidistantly from the XDATCAR file. Next, carry out ab-initio calculations for these structures. Be very careful to use exactly the same ab-initio parameters that were used for training. Otherwise in the worst case, one would compare apples with oranges. The longer the trajectory and the higher the number of chosen structures the better the testing, but of course at a higher computational cost due to the increased number of MD steps and ab-initio calculations.
Error analysis using py4vasp
For a comprehensive error analysis, compare ab-initio forces, stress, and energies with MLFF predictions. Below is a code snippet utilizing py4vasp to guide your analysis:
from py4vasp import MLFFErrorAnalysis from py4vasp import plot import numpy as np # Compute the errors mlff_error_analysis = MLFFErrorAnalysis.from_files( dft_data="./test_set/DFTdata/*.h5", mlff_data="./e01_error_analysis/MLFF_data/*.h5" ) energy_error = mlff_error_analysis.get_energy_error_per_atom() # force_error = mlff_error_analysis.get_force_rmse() # stress_error = mlff_error_analysis.get_stress_rmse() x = np.arange(len(energy_error)) plot(x, energy_error, ylabel="Energy error [eV/atom]", xlabel="Configuration Number")
Agreement check on physical properties
Assess the agreement between ab-initio reference and MLFF by testing specific physical properties. Consider properties like radial distribution functions, relaxed lattice parameters, phonons, elastic constants, relative energies of phases and defect formation energies, to name a few.
Application
When running force-field-only calculations (ML_MODE=RUN) set the ab-initio parameters to small values (this is automatically done for some tags, i.e. ENCUT). VASP cannot circumvent the initialization of KS orbitals although they are not used during the molecular dynamics run with machine learning.
Monitoring MLFF run with blocked averages
In each application, it is essential to carefully control the ensemble conditions, such as temperature, pressure, and volume. Achieving a specific condition requires allowing the system sufficient time to relax, typically measured in a minimum number of molecular dynamics steps. Determining the appropriate number of these steps becomes a crucial consideration in the optimization of MD simulations. Ideally, one could look directly at the observable or its mean value and observe that after a given number of steps the observable would not change anymore. Unfortunately, this is not easy in many cases since observables like temperature, pressure, and volume undergo many fluctuations. An alternative way to monitor the convergence of the observables is via statistical methods. For that block averages are a very good method. Explaining the method here would go beyond the scope of this paragraph, but the theory and the implementation of the method are nicely explained in appendix D3 of Ref. [1]. At the moment the user has to implement this post-calculation analysis himself, but we strongly advise to do so. The requirement of having properly relaxed structures is further intensified for advanced molecular-dynamics sampling methods.
Performance
The machine learning code is parallelized using MPI. It is most efficient if scaLAPACK is used since storing (and working on) large matrices, in particular the design matrix, will then be distributed over the MPI ranks. However, a LAPACK-only version exists as well. In the latter case, only a few matrices are stored in a distributed fashion, so due to the high memory demand, the LAPACK version is not feasible for "realistic" systems.
Computational efficiency in production runs
This section addresses challenges encountered in production runs utilizing the force field (ML_MODE=RUN) with the fast version (requiring prior refitting using ML_MODE=refit). The time required to evaluate a single step of this force field typically matches the duration needed to write results to files. Furthermore, the file-writing process operates solely in a serial manner. As the number of computational cores increases, the overall time for force field evaluation decreases, while the file-writing time remains constant. Therefore, optimizing performance necessitates adjusting the output frequency. The following flags can be used for that:
- ML_OUTBLOCK: This tag determines the minimum step interval for the following output file updates (OSZICAR, OUTCAR, XDATCAR, PCDAT, HDF5 and stdout). This tag will possibly change the value of NBLOCK, since NBLOCK is calculated as MAX(ML_OUTBLOCK, NBLOCK). For large trajectories this tag prevents unnecessarily large output files by controlling data output frequency.
- NBLOCK: This tag controls the frequency of the output of PCDAT and XDATCAR. As written above this tag has at least the same value as ML_OUTBLOCK. By setting this tag larger than ML_OUTBLOCK the writing of the PCDAT and XDATCAR will be less frequent than the writing of the remaining files.
- ML_OUTPUT_MODE: By setting this tag to 0 the calculation and output of the pair correlation function can be completely turned off.
Memory consumption
For optimal performance, the code employs different array distribution and parallelization strategies in different places. Many parts are optimized for scaLAPACK employing a block-cyclic distribution. For these parts, the memory usage per core should drop off linearly with the number of cores. In particular, the design matrix and covariance matrix are stored in this distributed fashion. In some parts of the code, however, large arrays of data are duplicated on every MPI rank. This is done for performance reasons, but can quickly lead to prohibitively large memory consumption (a few Gbs per core), especially on nodes with many cores. To address this problem we have implemented the possibility to store these arrays in shared memory. Then each node writes these arrays once in memory, but all cores on that node have reading access to these arrays. We strongly recommend activating this feature by adding the following precompiler option to the list of precompiler options: -Duse_shmem.
The estimated memory is usually found in the first section of the ML_LOGFILE and contains an estimation of memory requirements based on VASP files read on startup. In the simplest case (ML_MODE=TRAIN with no ML_AB file present) it depends on the settings in the INCAR and POSCAR file. For example, the expected memory consumption may strongly vary with the number of elements present in the POSCAR file. Various INCAR tags also influence the memory demand. The two most important are ML_MB and ML_MCONF. Continuation runs (ML_MODE=TRAIN with ML_AB file present) and refitting runs (ML_MODE=REFIT), additionally need to store the information from the ML_AB, which can be substantial.
A sample output for the memory estimation from the ML_LOGFILE looks as follows:
* MEMORY INFORMATION *********************************************************************************************************************** Estimated memory consumption for ML force field generation (MB): Persistent allocations for force field : 516.9 | |-- CMAT for basis : 20.3 |-- FMAT for basis : 458.5 |-- DESC for basis : 2.6 |-- DESC product matrix : 2.3 Persistent allocations for ab initio data : 8.1 | |-- Ab initio data : 7.8 |-- Ab initio data (new) : 0.3 Temporary allocations for sparsification : 460.9 | |-- SVD matrices : 460.7 Other temporary allocations : 15.5 | |-- Descriptors : 4.7 |-- Regression : 6.5 |-- Prediction : 4.2 Total memory consumption : 1001.4 ********************************************************************************************************************************************
While the individual items in the above listing are rather technical the most important number is given in the last line: Total memory consumption approximates the peak memory usage during this VASP run. However, since not all memory is always allocated at the same time the actual consumption may vary over time.
The following part summarizes which kind of parallelization each part employs:
scaLAPACK shared memory CMAT for basis x x FMAT for basis x DESC for basis x x DESC product matrix x Ab initio data Ab initio data (new) SVD matrices x Descriptors Regression x Prediction
The parts marked with an x for scaLAPACK contain block-cyclic distributed arrays that usually scale almost perfectly with the number of employed processors. The user will see that by increasing the number of processors the amount of memory needed will significantly drop for that part (we note that also Descriptors and Prediction will drop in memory, but only slightly since only minor parts of these are distributed). The parts marked with an x for shared memory show also a significant decrease in memory usage if the code is compiled for shared memory (precompiler option use_shmem).
| Mind: This is only an estimate, the actual memory requirement may be even higher. Moreover, this is only the usage for the machine learning part of VASP which in a training run adds up to the memory of the ab-initio part. |
| Mind: The most memory-consuming parts (design matrix, covariance matrix) are well distributed over multiple nodes. Hence if one runs out of memory one should try increasing the number of used nodes until the job fits into the combined memory of all nodes. |
Reduction of memory consumption in on-the-fly calculations
On-the-fly learning can be a very memory-intensive task since both the machine learning and the ab-initio calculations have to share the available memory simultaneously. This is especially true for systems with an increasing number of elements (4 or more) because the number of local reference configurations has to be sampled for each element.
Here is something to try to make the on-the-fly sampling part less memory-consuming:
- Minimize the ab-initio parameters required for converged results. Many times the parameters are way past the value that is required for convergence and hence setting these parameters to high values can put a substantial computational overhead on the calculation. In our experience, the following parameters are most likely to fall victim to oversetting: ENCUT, PREC, and number of k-points.
- If possible use more computational nodes to expand the overall available memory.
- Sample (ML_MODE=train) only with a low number of maximum local reference configurations that are just enough to keep the trajectories intact for sampling: ML_MB=500-1000.
- After the previous step the force-field is most likely of low accuracy. This can result in a high Bayesian error prediction and a too high sampling of training structures. A solution for that is to increase the Bayesian threshold ML_CTIFOR. For that first change the Bayesian error criterion such that it is constant during the calculation by setting ML_ICRITERIA=0. Next look for the values of the Bayesian errors in the ML_LOGFILE with
grep BEEF ML_LOGFILE. Set ML_CTIFOR such that only a given percentage of the Bayesian errors would be above this value. - At this point one has a force field with low accuracy.
- To get an accurate force field (re)select the number of local reference configurations. For this set ML_MODE=select and increase the maximum number of local reference configurations ML_MB. This step needs much more memory but the entire memory is available for the machine learning part since no ab-initio calculations are carried out.
- Last as usual do the refit with ML_MODE=refit.
Example
Sample input for learning of liquid water in the NpT ensemble at 0.001 kB using a temperature ramp.
ENCUT = 700 #larger cutoff LASPH = .True. GGA = RP IVDW = 11 ALGO = Normal LREAL = Auto ISYM = 0 IBRION = 0 MDALGO = 3 ISIF = 3 POTIM = 1.5 TEBEG = 200 TEEND = 500 LANGEVIN_GAMMA = 10.0 10.0 LANGEVIN_GAMMA_L = 3.0 PMASS = 100 PSTRESS = 0.001 NSW = 20000 POMASS = 8.0 16.0 ML_LMLFF = .TRUE. ML_MODE = TRAIN
- ENCUT: A larger plane-wave cut-off is used to accommodate possible changes in the lattice parameters because an NpT ensemble is used (ISIF=3).
- POMASS: Since this structure contains Hydrogen, the mass of Hydrogen is increased by a factor of 8 to be able to use larger integration steps POTIM. Without this one possibly needs to use integration steps of POTIM<0.5 hugely increasing the computation time.
- Here GGA=RP together with IVDW=11 is used which gives a good electron exchange and correlation description for liquid water.
LA 1 2 0 LA 1 3 0 LA 2 3 0 LR 1 0 LR 2 0 LR 3 0 S 1 0 0 0 0 0 0 S 0 1 0 0 0 0 0 S 0 0 1 0 0 0 0 S 0 0 0 1 -1 0 0 S 0 0 0 1 0 -1 0 S 0 0 0 0 1 -1 0
- Since a liquid in the NpT ensemble is simulated here, the ICONST file ensures that the lattice parameters are allowed to change to accommodate the pressure, but the length ratio and angles between the lattice parameters remain constant. This prevents unwanted deformations of the cell.
H2O_liquid
1.00000000000000
12.5163422232076691 0.0000233914035418 0.0000148478021513
0.0000000000114008 12.5162286489880472 0.0000199363611203
0.0000000000209813 0.0000000000005105 12.5176610723470780
H O
126 63
Direct
0.2282617284551465 0.0100328590137529 -0.1126387890656106
0.9746403004006459 -0.2476460083611154 -0.2607428157584675
0.5495157277709571 0.8457364197593650 -0.2477873147502692
0.8285605776747957 1.3957130438711647 0.3236429564827718
0.7772914822330327 0.4827858883979471 0.6904243173615018
0.0577768259920047 0.2223168123471880 -0.7608749959673696
0.9446580715027482 1.1212973211581765 0.3550426042339572
0.8506873790066947 0.1718425528358722 0.6288341575238712
0.6762596340888892 0.6505044169314104 0.2894195166948972
0.5611370443226182 -0.0333524123727857 0.5214208317960167
0.6816550720303126 -0.1211211829857703 0.4073898872723471
0.9980109015831524 0.4469736864199069 0.7701748771760492
0.6678832112330954 0.5234479361650100 0.1656392748166443
0.5040346446185426 0.5390736385800624 0.3470193329922442
0.6410360744431883 1.2034330133853826 -0.5204809500538871
0.5009140032853824 1.0194465602602765 0.0680968735186743
1.1286687923693957 0.4815796673077014 0.1056405447614227
1.3281242572016398 -0.0586744504576348 1.2791126768723411
1.2745979045721432 0.6605001257033906 0.1708686731589134
0.4889175843208496 0.3992133071729653 0.6662361557283188
1.1680688935402925 0.7448174915883062 0.4840737703429457
0.5441535549963540 1.2562238170486451 -0.1933215921435651
0.7539782822013665 0.4393165162255908 -0.1111210880770900
0.7158370742172643 0.2516648581738293 0.0129481804279206
0.2713582658190841 0.2279864583332417 -0.2165119651431964
0.9024539921023629 -0.1184662408708287 0.6213800486657953
0.4615161508482398 0.2475213172787736 0.4504737358928211
1.0118559400607643 0.7424282505541469 0.0746984790656740
0.2903967612053814 0.3755361842352651 0.5760967580335238
0.3231287130417146 0.7657698148287657 -0.4355073700974863
1.0376988097955901 0.0758439375796752 -0.0755636247212518
0.3490021766854268 -0.0144512406004137 -0.1286563387493205
0.9105647459905236 0.7180137269788829 -0.1630338422998813
0.6217984736501840 0.7636375746785418 -0.2985814512057716
0.7745581203120666 1.3708044347688073 0.2161898767275624
0.6604329281507487 0.4588369178206191 0.6638505715678867
0.9367092142161492 0.2566478031322914 -0.7657152701827817
0.9210696992439242 1.0100086011945200 0.3831186344742445
0.7198461947247682 0.1832700676815498 0.6289634217232680
0.5794490968641994 0.6650526418110994 0.2084878611072036
0.4451295011889302 0.0227193097626150 0.5285299460037345
0.6493078638087474 -0.2119508709082261 0.4952750816523580
0.9786031188935814 0.5691499073939285 0.7498421879775161
0.7284271721290199 0.4873101999963645 0.0606006569966631
0.4910977185777734 0.5607404559463554 0.4688446654579101
0.5685724756690831 1.1303057766954432 -0.4520626434287254
0.5834889098964630 0.9606882347596553 0.0036536368035990
1.0401204359334022 0.5623696717124362 0.0540990885930118
1.2824173065014235 0.0145062237175715 1.3666813391539134
0.3486617682267537 -0.2934149709168444 0.0822130144717180
0.5730104678470570 0.3084776512554136 0.6220956625895938
0.0696111366994306 0.7429990748207962 0.4037397615014190
0.5502677722150517 1.2295680823859727 -0.0773553830031266
0.6629391487219132 0.5328361705119534 -0.1150519950062741
0.6250848388543612 0.3083123187101773 0.0765665590910336
0.3662802395551557 0.2702906914452067 -0.1383165019423200
0.9736705556543800 -0.1799052283389148 0.5343666577034214
0.4295248327300012 0.3704736742659817 0.4332641348308674
0.8980973959825628 0.6990554008415506 0.0343927673672955
0.2875819013957733 0.4057639685103899 -0.3043930746820226
0.2339822436285078 0.7745846329456394 0.6458551118383669
1.0595055035190402 -0.0564894402119362 -0.0902725095487327
0.8934974071042586 0.3290512561302191 0.8603972804418396
0.5553026810346389 0.6918749861685528 0.8648052870098396
0.7595162123757241 0.2391418457892084 0.3402576351144293
0.1473261899861980 0.3709222233120330 0.4682213790034302
0.1421840618221771 0.3140746572683427 -0.1121762131537217
1.3389241568069978 0.3988616347426453 0.1635703018210843
-0.2448915061544370 0.7563953018862059 -0.0736150977487566
0.7590706624915531 0.4910146399954628 0.4684780730777085
0.7950571409085634 0.7192143646959017 0.5985905369710599
0.1316279824003455 1.0999687910648197 0.7533188747497124
0.1904139474335156 0.7791943520426338 0.0571106523349340
1.2220229066248534 0.3192108772536086 0.2369051680927172
0.3612775881033622 0.0855989478292645 0.1403208309917672
-0.1361272699805649 0.6820997653177969 0.2354821840318570
0.4087521084198726 0.5912825002582747 0.6358439098196149
0.1239762404674222 0.7546282143520640 -0.2004037475678275
0.3254524437469295 0.5629691201597067 0.3724966107408161
0.4753895829795802 1.0167551557396182 0.7120469261102015
0.2608638376650217 1.0575489302906138 0.5689964057513199
0.1643499778763993 0.9878520821198175 0.2274680280884254
0.5044272836232667 -0.1889898057206633 1.0969173862764161
1.0108484544264800 0.2499932639019371 -0.0323289029244656
1.4604847395188030 -0.1857921072604787 0.3648781664672482
-0.0676389676130162 -0.0295362893506241 0.7871165868504495
0.4846115199200384 0.2254773218591808 0.1655080485768635
0.7546930244801831 0.9283849256193616 0.8541595795735338
0.9706434056979190 1.1154826414004460 0.5267461552592998
-0.0861615702697154 -0.1809840616227028 -0.6553434728259054
0.8442013982186719 -0.0307048052283226 0.1425354846866949
0.6887583721043200 1.0654555145745237 0.2683125737537906
1.0027728188337521 0.5023071178777798 -0.4225836976328659
1.2932985504962016 1.5692646782719462 0.9368592413035413
0.4716460351076925 0.6993549392273799 0.6601847017954563
0.2065050455598290 0.8340729505249687 -0.1549365584796285
0.7134717637166987 0.6306375489985552 0.5979355450208014
0.1305819547597963 1.1628983978276421 0.6489352069792226
0.1272197155625575 0.8779790277321273 0.1016609192978390
1.2490179100185559 0.1997381130828568 0.2661804901290689
1.3538940004316671 0.0865346934520785 0.0162268012094167
-0.1648144254795892 0.6328837747686877 0.3517458960703262
1.3576963330025944 -0.2535471527532498 0.3451642885788545
-0.1512707063199035 0.0447723975378184 0.7370562480777335
0.2082920817694131 0.6238194842808575 0.3627405505637077
0.4818735663404834 0.0797305025898344 0.8149171190132681
0.2714920258235731 0.9437115667773756 0.5398585008814204
0.0598987571605861 1.0109519535694200 0.1622926257298793
0.5118223005328099 -0.2906673876063635 1.0219508170746381
0.9862800303912808 0.1828001523416312 0.0677466130856736
1.0595449212229817 0.5431076873367398 -0.5303300708777712
1.2934388789888798 0.6286357417906868 -0.1682875581053126
0.4618116975337169 0.2958921133995223 0.2670334121905841
0.7539636581184406 0.9360985551615451 -0.0248108921725196
0.9998082474973725 1.2364748213827927 0.5458537302387204
0.0084172701408917 -0.0989295133906621 -0.6906681930981559
0.9033157610523457 -0.1303930279825006 0.1228072425414686
0.6604461112340703 0.9892487041136045 0.1825505778817879
0.7885276375808787 0.6294686108635517 -0.0737926736153585
0.8840546243663174 0.5053739463625377 0.4526376410385395
0.8074749932462770 0.2947711469591280 0.7787234411725377
0.4632367138215856 0.6097289940035490 -0.1145492866143238
0.7775247539743841 0.1357560792893380 0.4055163611357055
0.2117515661833950 0.2832304177268588 0.4122050502626490
0.0768107057290735 0.4027427851525467 -0.0515166562421230
1.2669405505626230 0.4880120983162565 0.2202021018146102
0.2919481531025963 -0.0097036832216508 -0.0729957055081244
0.9840898695695925 0.7046088238612841 -0.1980300785209053
0.5582639462588442 0.7673812911725254 -0.2587733472825737
0.8220678952661906 1.3361683524558097 0.2699860947274584
0.7257118638315225 0.4999486906307656 0.6412374880809832
-0.0159466690459744 0.1935938619023044 -0.7768095097490648
0.9155392077434708 1.0805930191162569 0.4138690591165022
0.7862174758070717 0.1816706702550143 0.6732485622988889
0.6132430910865457 0.6183045290387048 0.2587122784691759
0.5240798045171384 0.0270658373485661 0.5490772798003927
0.6227258931836714 -0.1513468939644967 0.4514026249947363
0.9638867643770986 0.4954513053854325 0.7212510085139069
0.7159100053950270 0.4678155943640417 0.1349439087134111
0.4582333315581760 0.5168500155232567 0.4094860848574138
0.6020128307710225 1.2064430441579375 -0.4506555458643959
0.5521951499401644 0.9590467759911693 0.0741168885795418
1.0781674762106039 0.4954947302196762 0.0441857869962515
1.2877834938552375 0.0081337644237061 1.2888612376304034
1.2732518381606885 -0.3103063836930492 0.0984742851109190
0.5595086990259246 0.3696506726448117 0.6743217671307982
0.1240887034225702 0.6960193789405823 0.4337932939025890
0.5086138696669937 1.2114646205434219 -0.1402693575758740
0.7313300345574206 0.5088192316865796 -0.0848414107423346
0.6392500541546888 0.2452966478859945 0.0290217369836307
0.2906220813433669 0.2834501467738138 -0.1612157326655933
0.9265368908511590 -0.1886857109185944 0.5950530730285820
0.4191322585983637 0.2968514680208339 0.4065358381730697
0.9503223312345728 0.6924078287564821 0.0976010227803059
0.3171226540194806 0.4277726129695098 0.6291827895026040
0.2523597102929802 0.7992029127084535 -0.4251410697001895
1.0542894643082081 0.0098095875712209 -0.1254405527744111
-0.1850276732646079 0.7064002231521372 -0.0809385398102708
0.8146436675316787 0.5091462597700946 0.4152356140927696
0.8203699138320668 0.3369968354028824 0.8455921310438892
0.5350509729728494 0.6295527668603674 0.9102304780657455
0.7193764908855955 0.1838347476185205 0.3819141293957220
0.1910314352006382 0.3094472630165150 0.4823838977521944
0.0687276874475614 0.3407534564140682 -0.0961793949793184
1.2668203814128003 0.4259424135404398 0.1731136054217358
0.4280856307534187 0.6584589779898570 0.6012619513268567
1.1963611411889725 0.7804022094739607 -0.2110274995492418
0.7214250257605557 0.7065604538172952 0.5794991635695482
0.1776849231487917 1.1234852797096138 0.6937893559514705
0.1285406853584958 0.8283735895779946 0.0360212378784548
1.1982000164502744 0.2527276897017764 0.2755163953762200
0.3971884946158640 0.1135585073114126 0.0762033607013268
-0.1677109438487009 0.6976010251448760 0.3070009760429893
1.3843291659064216 -0.1806544740790267 0.3487638347163066
-0.1370877275115541 -0.0294965108434674 0.7526972827056088
0.2742057504147322 0.5976400628879622 0.3238891214955297
0.4681381611246405 1.0080818685930206 0.7875962423618043
0.2988391245755818 1.0128379546679014 0.5215141172374251
0.0979325070909129 0.9559351747734792 0.2036472418484847
0.4871098095650768 -0.2661593993271190 1.0958159235212488
0.9840996652256983 0.1761359392656111 -0.0086227132193279
1.0181722221064600 0.4832974111083591 -0.4993793874483681
1.3336737594231565 0.5733445036683216 0.8701294276086065
0.4805509314794579 0.2981571227457179 0.1930037183242462
0.7146125697156993 0.8998617569525493 0.9145452976881076
0.9916627840023351 1.1683363103812550 0.5804316669886708
-0.0389136332191330 -0.1241670083541440 -0.6326131437048044
0.8956869974284227 -0.0586980011006573 0.0867714766274296
0.7097227556462733 0.9934862114531017 0.2391419679113634
Related articles
Machine-learned force fields, Ionic minimization, Molecular dynamics, Machine learning force field calculations: Basics