ACFDT/RPA calculations: Difference between revisions
| (27 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
The adiabatic-connection-fluctuation-dissipation theorem ( | The adiabatic-connection-fluctuation-dissipation theorem (ACFDT) can be used to derive the random-phase approximation (RPA). | ||
The ACFDT-RPA ground-state energy <math>E_{\mathrm{RPA}}</math> is the sum of the ACFDT-RPA correlation energy <math>E_{c}</math> and the Hartree-Fock (HF) energy <math>E_{\mathrm{EXX}}</math> evaluated non self-consistently using Kohn-Sham orbitals computed within density-functional theory (DFT): | The ACFDT-RPA ground-state energy <math>E_{\mathrm{RPA}}</math> is the sum of the ACFDT-RPA correlation energy <math>E_{c}</math> and the Hartree-Fock (HF) energy <math>E_{\mathrm{EXX}}</math> evaluated non self-consistently using Kohn-Sham orbitals computed within density-functional theory (DFT): | ||
| Line 8: | Line 8: | ||
If {{TAG|ALGO}}=RPA is set in the {{TAG|INCAR}} file, VASP calculates the correlation energy within RPA. To this end, VASP first calculates the independent-particle response function, using the unoccupied states given in the {{TAG|WAVECAR}} file, and then determines the correlation energy using the plasmon-fluctuation equation: | If {{TAG|ALGO}}=RPA is set in the {{TAG|INCAR}} file, VASP calculates the correlation energy within RPA. To this end, VASP first calculates the independent-particle response function, using the unoccupied states given in the {{TAG|WAVECAR}} file, and then determines the correlation energy using the plasmon-fluctuation equation: | ||
<math>E_{c} = \frac{1}{2 \pi} \int_{0}^{\infty} | <math>E_{c} = \frac{1}{2 \pi} \int_{0}^{\infty}[ \mathrm{Tr} \, \ln(1-\chi( {\rm i} \omega) V) + \chi( {\rm i} \omega) V ]\, d \omega</math>. | ||
More information about the theory behind the RPA is found [[RPA/ACFDT: Correlation energy in the Random Phase Approximation|here]]. | More information about the theory behind the RPA is found [[RPA/ACFDT: Correlation energy in the Random Phase Approximation|here]]. | ||
| Line 27: | Line 27: | ||
{{NB|warning| The convergence of DFT eigenenergies influences the convergence of the RPA correlation energy.|:}} | {{NB|warning| The convergence of DFT eigenenergies influences the convergence of the RPA correlation energy.|:}} | ||
{{NB|tip|Use the Perdew-Burke-Ernzerhof (PBE) pseudopotentials with a small {{TAG|EDIFF}} and avoid {{TAG|ISMEAR}}>0.|:}} | {{NB|tip|Use the Perdew-Burke-Ernzerhof (PBE) pseudopotentials with a small {{TAG|EDIFF}} and avoid {{TAG|ISMEAR}}>0.|:}} | ||
:The DFT run can be done with your favorite setup, but we recommend attaining very high precision (small {{TAG|EDIFF}} tag) and to use a small smearing width ({{TAG|SIGMA}} tag), and to avoid higher-order Methfessel-Paxton smearing (see also {{TAG|ISMEAR}}). That is because Methfessel-Paxton smearing can lead to negative one-electron occupancies, which can result in unphysical correlation energies. We suggest using [[GGA|PBE]] orbitals as input for the ACFDT-RPA run, but other choices, e.g., local-density-approximation (LDA) or [[:Category: | :The DFT run can be done with your favorite setup, but we recommend attaining very high precision (small {{TAG|EDIFF}} tag) and to use a small smearing width ({{TAG|SIGMA}} tag), and to avoid higher-order Methfessel-Paxton smearing (see also {{TAG|ISMEAR}}). That is because Methfessel-Paxton smearing can lead to negative one-electron occupancies, which can result in unphysical correlation energies. We suggest using [[GGA|PBE]] orbitals as input for the ACFDT-RPA run, but other choices, e.g., local-density-approximation (LDA) or [[:Category:Hybrid_functionals|hybrids]], are possible as well. For hybrid functionals, we suggest carefully considering the caveats mentioned in Ref. {{cite|paier:2008}}. Specifically, the RPA dielectric matrix yields too weak screening for hybrid functionals, which potentially deteriorates RPA results. | ||
'''Step 2:''' Compute the HF energy <math>E_{\mathrm{EXX}}</math> using the DFT orbitals. That is, e.g., | '''Step 2:''' Compute the HF energy <math>E_{\mathrm{EXX}}</math> using the DFT orbitals. That is, e.g., | ||
{{TAG|ALGO}} = EIGENVAL ; {{TAG|NELM}} = 1 | {{TAG|ALGO}} = EIGENVAL ; {{TAG|NELM}} = 1 | ||
| Line 79: | Line 79: | ||
=== Output of ACFDT-RPA total energy === | === Output of ACFDT-RPA total energy === | ||
The ACFDT-RPA total energy is calculated for 8 different | The ACFDT-RPA total energy is calculated for 8 different energy cutoffs and a linear regression is used to extrapolate the results to the infinite cutoff limit, see [[ACFDT/RPA calculations#basis_cutoff|section below]]. A successful RPA calculation writes the following lines into the {{FILE|OUTCAR}} file: | ||
cutoff energy smooth cutoff RPA correlation Hartree contr. to MP2 | cutoff energy smooth cutoff RPA correlation Hartree contr. to MP2 | ||
| Line 94: | Line 94: | ||
converged value -19.2585393615 -28.2627347266 | converged value -19.2585393615 -28.2627347266 | ||
Here, the third and fourth columns correspond to the correlation energy (for that specific cutoff | Here, the third and fourth columns correspond to the correlation energy (for that specific energy cutoff) in the RPA and the direct second-order Møller–Plesset (MP2) approximation, i.e., the second-order term in RPA. The corresponding results of the linear regression are found in the line starting with <code>converged value</code>. | ||
<span id="ACFDTR/RPAR"> | <span id="ACFDTR/RPAR"> | ||
| Line 132: | Line 132: | ||
The line <code>HF+RPA corr. energy TOTEN</code> contains the total energy calculated with the largest cutoff {{TAG|ENCUTGW}}. | The line <code>HF+RPA corr. energy TOTEN</code> contains the total energy calculated with the largest cutoff {{TAG|ENCUTGW}}. | ||
The line <code>HF+E_corr(extrapolated)</code> contains the total energy with the extrapolated value for the RPA correlation energy. | The line <code>HF+E_corr(extrapolated)</code> contains the total energy with the extrapolated value for the RPA correlation energy. | ||
=== Singles contribution to the correlation energy === | |||
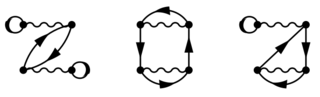
The low-scaling RPA algorithm also allows for the determination of the so-called singles contribution,{{cite|klimes:jcp:143}}{{cite|ren:prb:88}} to the total energy represented by following diagrams: | |||
[[File:SinglesDiagrams.png|320px]] | |||
In most textbooks{{cite|mattuck:2012}} this contribution is assumed to be zero. Ren et al.{{cite|ren:prb:88}} pointed out that this is true only in the Hartree-Fock basis set. The singles contribution is non-vanishing for other basis sets. | |||
The singles contribution is calculated for {{TAG|LSINGLES}}=.TRUE.. In this case following additional lines can be found in OUTCAR: | |||
HF single shot energy change -1.23182672 | |||
renormalized HF singles -1.23310555 | |||
Here, the first line contains the value of the singles as proposed by Klimeš et al.,{{cite|klimes:jcp:143}} while the second line contains the singles contribution of Ren et al.{{cite|ren:prb:88}}. In most cases we found that the two values are exceedingly close to each other, which can be understood in the way how the propagator is renormalized.{{cite|klimes:jcp:143}} | |||
<span id="RPAFORCES"> | <span id="RPAFORCES"> | ||
=== Optional: RPA Forces === | === Optional: RPA Forces === | ||
| Line 152: | Line 164: | ||
-0.00958461 -0.00958461 0.13485779 0.04179056 0.04179056 0.00283088 | -0.00958461 -0.00958461 0.13485779 0.04179056 0.04179056 0.00283088 | ||
0.25787833 0.25787833 0.22191754 -0.04337198 -0.04337198 0.00431513 | 0.25787833 0.25787833 0.22191754 -0.04337198 -0.04337198 0.00431513 | ||
{{ | |||
The suggested updated positions are also written to the CONTCAR file (if {{TAG|NSW}}=0). The updated positions are obtained by multiplying the RPA-forces with the parameter {{TAG|DAMP_NEWTON}} and the inverse of the DFT-Hessian (which is also calculated during the RPA force calculations) and adding the resultant vector to the current positions. {{TAG|DAMP_NEWTON}} currently defaults to 0.8, but the user might want to change this to 1.0 (no damping), or smaller values if instabilities are observed. The CONTCAR file can be copied to the POSCAR file, and a few such RPA calculations should recover the groundstate structure. Alternatively, standard relaxations ({{TAG|IBRION}} =1-4) or even MD's can be performed. | |||
</span> | </span> | ||
=== Caveats: Noise in Energies and RPA Forces === | |||
Generally, the energy calculated by the RPA can be quite noisy as a function of the ionic positions, in particular, if {{TAG|PRECFOCK}} = FAST and {{TAG|NMAXFOCKAE}} = 1 is set (these are the default values for RPA calculations). Most of the noise is related to the exact exchange energy. To determine if noise is affecting the results, it is useful to calculate the exchange energy separately as explained in step 2 above. If the exchange energy reported there is smooth, and the exchange energy reported by the all-in-one approach is noisy (e.g. shows odd jumps as a function of the positions or volume), it is strongly recommended to consider one or both of the options discussed below. | |||
Currently, to reduce the noise in the energy and forces, it is sensible to set {{TAG|PRECFOCK}} = Normal (typically doubling the execution time and memory requirement). It is also possible to set {{TAG|LMAXFOCKAE}} = -1 (which implicitly sets {{TAG|NMAXFOCKAE}} = 0). This makes the correlation energies and the related forces less noisy, but technically less accurate (i.e. part of the correlation energy will be missing at high transition energies). Overall, RPA forces must be used carefully and only after extensive testing of all relevant parameters. | |||
=== Memory bottleneck and Parallelization === | === Memory bottleneck and Parallelization === | ||
{{ | |||
The cubic scaling space-time RPA algorithm requires considerably more memory than the corresponding quartic-scaling implementations, two Green's functions <math>G({\bf r,r'},i\tau_n)</math> have to be stored in real-space. To reduce the memory overhead, VASP exploits Fast Fourier Transformations (FFT) to avoid storage of the matrices on the (larger) real space grid, on the one hand. The precision of the FFT can be selected with {{TAG|PRECFOCK}}, where usually the values ''Fast'' sufficient. | |||
On the other hand, the code avoids storage of redundant information, i.e., both the Green's function and polarizability matrices are distributed as well as the individual imaginary grid points. The distribution of the imaginary grid points can be set by hand with the {{TAG|NTAUPAR}} and {{TAG|NOMEGAPAR}} tags, which splits the imaginary grid points {{TAG|NOMEGA}} into {{TAG|NTAUPAR}} time and {{TAG|NOMEGAPAR}} groups. For this purpose both tags have to be divisors of {{TAG|NOMEGA}}. | |||
The default values are usually reasonable choices provided the tag {{TAG|MAXMEM}} is set correctly and we strongly recommend to set {{TAG|MAXMEM}} instead of {{TAG|NTAUPAR}}. | |||
{{NB|important|As of version 6.2, {{TAGBL|MAXMEM}} is estimated automatically (if not set) from the "MemAvailable" entry of the Linux kernel in "/proc/meminfo".}} | |||
The required storage for a low-scaling RPA or GW calculation depends mostly on {{TAG|NTAUPAR}}, the number of MPI groups that share same imaginary time points. A rough estimate for the required bytes is given by | |||
(NGX*NGY*NGZ)*(NGX_S*NGY_S*NGZ_S) / ( NCPU / {{TAGBL|NTAUPAR}} ) * 16 | |||
where "NCPU" is the number of MPI ranks used for the job,"NGX,NGY,NGZ" denotes the number of FFT grid points for the exact exchange and "NGX_S,NGY_S,NGZ_S" the number of FFT grid points for the supercell. Note, both grids are written to the {{TAGBL|OUTCAR}} file after the lines | |||
FFT grid for exact exchange (Hartree Fock) | |||
FFT grid for supercell: | |||
The smaller {{TAG|NTAUPAR}} is set, the less memory per node the job requires to finish successfully. | |||
The approximate memory requirement is calculated in advance and printed to screen and {{TAGBL|OUTCAR}} as follows: | |||
min. memory requirement per mpi rank 1234 MB, per node 9872 MB | |||
</span> | </span> | ||
| Line 176: | Line 217: | ||
{{:Basis set convergence of RPA-ACFDT calculations}} | {{:Basis set convergence of RPA-ACFDT calculations}} | ||
Convergence with respect to the number of plane waves can be rather slow, and we recommend to test the calculations carefully. Specifically, the calculations should be performed at the default energy cutoff {{TAG|ENCUT}}, and at an increased cutoff (ideally the default energy cutoff <math>\times 1.3</math>). Another issue is that energy volume-curves are sometimes not particularly smooth. In that case, the best strategy is to set | Convergence with respect to the number of plane waves can be rather slow, and we recommend to test the calculations carefully. Specifically, the calculations should be performed at the default energy cutoff {{TAG|ENCUT}}, and at an increased cutoff (ideally the default energy cutoff <math>\times 1.3</math>). Another issue is that energy volume-curves are sometimes not particularly smooth. In that case, the best strategy is to set | ||
{{TAGBL|ENCUT}} = 1.3 times default cutoff | {{TAGBL|ENCUT}} = 1.3 times default energy cutoff | ||
{{TAGBL|ENCUTGWSOFT}} = 0.5 times default cutoff energy | {{TAGBL|ENCUTGWSOFT}} = 0.5 times default energy cutoff | ||
where the default energy cutoff is the usual one (maximum ENMAX in POTCAR files). The frequency integration also needs to be checked carefully, in particular for small gap systems (some symmetry broken atoms) convergence can be rather slow, since the one-electron band gap can be very small, requiring a very small minimum <math>\omega</math> in the frequency integration. | |||
=== K-point convergence: Spline interpolation === | |||
{{NB|mind|{{TAG|ESF_SPLINES}} is available as of VASP.6.5.0}} | |||
It is possible to use spline interpolation to improve upon k-point integration errors by rewriting the | |||
RPA correlation energy as an integral | |||
<math> | |||
E_c^{{\rm RPA}}= \sum_{{\mathbf{q}}\in \mathbf{BZ} }\sum_{{\mathbf{G}}} S({\bf q+G}) | |||
</math> | |||
over the electronic structure factor: | |||
<math> | |||
S({\bf q}+{\bf G}) =\int {\rm d}\omega | |||
\left\{(\mathrm{ln}[1-\tilde\chi^0({\mathbf{q}},\mathrm{i}\omega)V({\mathbf{q}})])_{{\mathbf{G,G}}} +V_{{\mathbf{G,G}}}({\mathbf{q}})\tilde\chi^0({\mathbf{q}},{\mathrm{i}}\omega) \right\} | |||
</math> | |||
If {{TAG|ESF_SPLINES}}=T is set, the code stores the electronic structure factor on a coarse grid defined by {{FILE|KPOINTS}} and performs a tricubic spline interpolation towards finer q-grids iteratively. After each iteration the RPA correlation energy is evaluated and compared to the result of previous interpolation. | |||
If the difference in energy is smaller than {{TAG|ESF_CONV}} within {{TAG|ESF_NINTER}} interpolation steps, the code considers the q-point integration to be converged and reports the result to {{FILE|OUTCAR}} in the following format | |||
cutoff energy smooth cutoff RPA correlation Hartree contr. to MP2 RPA spline-interp. | |||
----------------------------------------------------------------------------------------------------- | |||
166.667 133.333 -12.9738715106 -19.7255874374 -13.4968000908 | |||
158.730 126.984 -12.8840657072 -19.6294580403 -13.4017404001 | |||
151.172 120.937 -12.7775593388 -19.5151822998 -13.3005326847 | |||
143.973 115.178 -12.6604147404 -19.3892142669 -13.1868498210 | |||
137.117 109.694 -12.5530911576 -19.2733151174 -13.0861120393 | |||
130.588 104.470 -12.4659186304 -19.1786165194 -12.9778587892 | |||
124.369 99.495 -12.3690601643 -19.0725742983 -12.8709666989 | |||
118.447 94.758 -12.2461267475 -18.9372318755 -12.7590723870 | |||
linear regression | |||
converged value -14.0340307585 -20.8751715586 -14.5828037654 | |||
The last column contains the result from the spline interpolation for the selected energy cutoffs reported in the first column. | |||
{{NB|warning|Delete {{FILE|WAVEDER}} for this method.}} | |||
Note that this method is incompatible with k-p perturbation theory, where the | |||
largest q-point integration error <math> | |||
\lim_{\bf q\to 0} \tilde\chi^0_{{\bf G G}'}({\bf q},{\rm i}\omega) \cdot {\bf V}_{\bf G G'}({\bf q}) | |||
</math> is added explicitly to the RPA integral. | |||
This long-wave contribution is stored in {{FILE|WAVEDER}}, and VASP assumes you want to add this term if the file is present in the working directory. | |||
Also, the long-wave limit is ill-defined for metallic systems, in contrast to the spline interpolation method. | |||
{{NB|mind|{{TAG|ESF_SPLINES}} can be used for metals.}} | |||
Nevertheless, for insulators, we still recommend using {{FILE|WAVEDER}} and not set {{TAG|ESF_SPLINES}} for efficiency reasons. | |||
</span> | </span> | ||
| Line 195: | Line 277: | ||
* {{TAG|MAXMEM}} sets the available memory per MPI rank on each node | * {{TAG|MAXMEM}} sets the available memory per MPI rank on each node | ||
* {{TAG|LFINITE_TEMPERATURE}} switches on Matsubara (finite temperature) formalism | * {{TAG|LFINITE_TEMPERATURE}} switches on Matsubara (finite temperature) formalism | ||
* {{TAG|ESF_SPLINES}} uses tricubic spline interpolation of electronic structure factor to accelerate k-point convergence | |||
== References == | == References == | ||
| Line 201: | Line 284: | ||
---- | ---- | ||
[[Category:Many- | [[Category:Many-body perturbation theory]][[Category:ACFDT]][[Category:Howto]][[Category:Low-scaling GW and RPA]] | ||
Latest revision as of 07:06, 20 December 2024
The adiabatic-connection-fluctuation-dissipation theorem (ACFDT) can be used to derive the random-phase approximation (RPA). The ACFDT-RPA ground-state energy is the sum of the ACFDT-RPA correlation energy and the Hartree-Fock (HF) energy evaluated non self-consistently using Kohn-Sham orbitals computed within density-functional theory (DFT):
.
Note that, here includes also the Hartree energy, the kinetic energy, as well as the Ewald energy of the ions, whereas often in literature refers only to the exact-exchange (EXX) energy evaluated using DFT orbitals.
If ALGO=RPA is set in the INCAR file, VASP calculates the correlation energy within RPA. To this end, VASP first calculates the independent-particle response function, using the unoccupied states given in the WAVECAR file, and then determines the correlation energy using the plasmon-fluctuation equation:
.
More information about the theory behind the RPA is found here.
General recipe to calculate ACFDT-RPA total energies
The ACFDT-RPA total energies can be computed in a four-step procedure or in an all-in-one approach. The all-in-one approach is available as of VASP.6 and can be done in one single step. Both procedures comprise a self-consistent DFT calculation, diagonalizing the KS Hamiltonian, and the RPA calculation itself. While the all-in-one approach is very convenient, there are several caveats discussed below.
Four-step procedure to calculate ACFDT-RPA total energy
This four-step procedure is the standard procedure in VASP.5, and is also available in VASP.6 by setting NBANDS in the RPA step.
Step 1: a standard DFT run.
- All occupied orbitals (and as usual in VASP, a few unoccupied orbitals) of the DFT Hamiltonian are calculated. For instance,
EDIFF = 1E-8 # required for convergence of RPA total energies ISMEAR = 0 ; SIGMA = 0.05
Warning: The convergence of DFT eigenenergies influences the convergence of the RPA correlation energy.
- The DFT run can be done with your favorite setup, but we recommend attaining very high precision (small EDIFF tag) and to use a small smearing width (SIGMA tag), and to avoid higher-order Methfessel-Paxton smearing (see also ISMEAR). That is because Methfessel-Paxton smearing can lead to negative one-electron occupancies, which can result in unphysical correlation energies. We suggest using PBE orbitals as input for the ACFDT-RPA run, but other choices, e.g., local-density-approximation (LDA) or hybrids, are possible as well. For hybrid functionals, we suggest carefully considering the caveats mentioned in Ref. [1]. Specifically, the RPA dielectric matrix yields too weak screening for hybrid functionals, which potentially deteriorates RPA results.
Step 2: Compute the HF energy using the DFT orbitals. That is, e.g.,
ALGO = EIGENVAL ; NELM = 1 LWAVE = .FALSE. ! WAVECAR not written LHFCALC = .TRUE. ; AEXX = 1.0 ! ALDAC = 0.0 ISMEAR = 0 ; SIGMA = 0.05
- Here, LWAVE = .FALSE. avoids an accidental update of the WAVECAR file. Also, VASP automatically sets ALDAC = 1-AEXX, i.e., for AEXX = 1.0, ALDAC = 0.0.
Tip: For insulators and semiconductors with a sizable gap, faster k-point convergence of the HF energy can be obtained by setting HFRCUT=-1, although this slows convergence for metals.
Step 3: Compute a sufficient number of unoccupied states.
- In the OUTCAR file of Step 1, search for
maximum number of plane-waves:and run VASP again with the following INCAR file to determine the unoccupied states by exact diagonalization of the KS Hamiltonian. The KS Hamiltonian must be the same as in step 1, which might be DFT or hybrid.
NBANDS = maximum number of plane-waves (times 2 for vasp_gam) ALGO = Exact ! exact diagonalization EDIFF = 1E-8 # required for convergence of RPA total energies LOPTICS = .TRUE. ISMEAR = 0 ; SIGMA = 0.05
- For calculations using
vasp_gam, that is the gamma-point only version of VASP, NBANDS must be set to twice themaximum number of plane-waves:found in the OUTCAR file of Step 1. For metals, we recommend to avoid setting LOPTICS=.TRUE., since this slows down k-point convergence .
Step 4: Calculate the ACFDT-RPA correlation energy.
NBANDS = maximum number of plane-waves ALGO = ACFDT NOMEGA = 12 ! default ISMEAR = 0 ; SIGMA = 0.05
- The number of imaginary-frequency and imaginary-time-grid points NOMEGA is usually set to 8-24. For large gap insulators NOMEGA = 8 will suffice, while for semiconductors 10-12 suffices.
Important: For VASP 6.X, NBANDS must be set in this step.
All-in-one approach to calculate ACFDT-RPA total energy
VASP will read the WAVECAR file, perform a self-consistent DFT calculation by iterating until convergence is reached, diagonalize the DFT Hamiltonian in the basis set spanned by all KS orbitals, and finally proceed with the RPA calculation. The all-in-one approach is only available as of VASP.6, and it is particularly convenient for the RPAR and GWR algorithms. An example INCAR file is
ALGO = RPAR EDIFF = 1E-8 # required for convergence of RPA total energies ISMEAR = 0 ; SIGMA = 0.05 NOMEGA = 8-24 ! for large gap insulators NOMEGA = 8 will suffice, for semiconductors 10-12 suffices LOPTICS = .TRUE. ! optional LPEAD = .TRUE. ! required for 6.1 and 6.2 if LOPTICS = .TRUE.
Warning: The convergence of DFT eigenenergies influences the convergence of the RPA correlation energy.
The head of the dielectric function can be calculated only for insulators by setting the LOPTICS tag and only the Perturbation-Expression-After-Discretization (PEAD) method is supported, see LPEAD. Furthermore, EDIFF should be small to calculate the DFT orbitals with high precision. Although it is not strictly required, we recommend starting the calculation from a well-converged DFT WAVECAR file.
There are several caveats to the all-in-one approach:
- There is no general support for ACFDT/RPA on top of hybrid functionals. In VASP 6.2, only LDA and gradient corrected functionals are supported. As of VASP 6.2, the all-in-one approach can be used for Hartree-Fock-type calculations, as well as hybrid functionals without range separation. However, range-separated hybrid functionals (including HSE, LMODELHF) yield erroneous results or potentially even crash. Please compare the total energies in a standard DFT/hybrid functional calculation against the energies obtained for the mean-field step in the all-in-one approach: The energies must be exactly the same. If they differ, fall back to the four-step procedure that is explained above.
- To select the new all-in-one approach, it is important "not to set NBANDS" in the RPA step. If NBANDS is set in the INCAR file, VASP.6 proceeds with reading the WAVECAR file found in the directory (if not present, random orbitals are used!), and then calculates the correlation energy using these orbitals and one-electron energies.
- The basis set used in the diagonalization is strictly given by all plane waves. That is, there is no option to reduce the basis set size as one can by setting NBANDS in Step 3 and Step 4 of the four-step procedure.
- The exchange energy is only calculated if the low-scaling RPA is selected.
- As of VASP 6.3, the head of the dielectric function (G=0 component) can be calculated by setting LOPTICS = .TRUE.
- In the all-in-one procedure, VASP automatically sets LMAXFOCKAE and NMAXFOCKAE. This changes the energies for hybrid functionals and Hartree-Fock slightly. Hence, you need to set LMAXFOCKAE = 4 also in Step 1 of the four-step procedure to obtain the same results as in the all-in-one procedure.
Output of ACFDT-RPA total energy
The ACFDT-RPA total energy is calculated for 8 different energy cutoffs and a linear regression is used to extrapolate the results to the infinite cutoff limit, see section below. A successful RPA calculation writes the following lines into the OUTCAR file:
cutoff energy smooth cutoff RPA correlation Hartree contr. to MP2
---------------------------------------------------------------------------------
316.767 316.767 -17.5265976349 -26.2640927215
301.683 301.683 -17.3846505665 -26.0990489039
287.317 287.317 -17.2429031341 -25.9344769084
273.635 273.635 -17.0686574017 -25.7325162480
260.605 260.605 -16.8914915810 -25.5277026697
248.195 248.195 -16.7202601717 -25.3302982602
236.376 236.376 -16.5559849344 -25.1415392478
225.120 225.120 -16.3635400223 -24.9210737434
linear regression
converged value -19.2585393615 -28.2627347266
Here, the third and fourth columns correspond to the correlation energy (for that specific energy cutoff) in the RPA and the direct second-order Møller–Plesset (MP2) approximation, i.e., the second-order term in RPA. The corresponding results of the linear regression are found in the line starting with converged value.
Low-scaling ACFDT/RPA algorithm
Virtually the same tags and procedures apply to the low-scaling RPA algorithm implemented in VASP 6 [2]. However, ALGO=ACFDT or ALGO=RPA needs to be replaced by either ALGO=ACFDTR or ALGO=RPAR.
With this setting VASP calculates the independent-particle polarizability using Green's functions on the imaginary time axis by the contraction formula [3]
Subsequently, a compressed Fourier transformation on the imaginary axes yields
The remaining step is the evaluation of the correlation energy and is the same as described above.
Crucial to this approach is the accuracy of the Fourier transformation from , which in general depends on two factors: First, the grid order that can be set by NOMEGA in the INCAR file. Here, similar choices as for the ALGO=ACFDT are recommended. Second, the grid points and Fourier matrix have to be optimized for the same interval as spanned by all possible transition energies in the polarizability. The minimum (maximum) transition energy can be set with the OMEGAMIN (OMEGATL) tag and should be smaller (larger) than the bandgap, i.e., the maximum transition energy, of the previous DFT calculation. VASP determines these values automatically and writes it in the OUTCAR after the lines
Response functions by GG contraction:
These values should be checked for consistency. Furthermore, we recommend inspecting the grid and transformation errors by looking for the following lines in the OUTCAR file
nu_ 1= 0.1561030E+00 ERR= 0.6327933E-05 finished after 1 steps nu_ 2= ... Maximum error of frequency grid: 0.3369591E-06
Every frequency point will have a similar line as shown above for the first point. The value after ERR= corresponds to the maximum Fourier-transformation error and should be of similar order as the maximum integration error of the frequency grid.
Output of low-scaling ACFDT/RPA
Selecting the low-scaling RPA algorithm, VASP computes the total energy in the RPA and writes the following output
----------------------------------------------------- HF-free energy FHF = -25.11173505 eV HF+RPA corr. energy TOTEN = -36.96463791 eV HF+E_corr(extrapolated) = -37.70506951 eV
The line HF+RPA corr. energy TOTEN contains the total energy calculated with the largest cutoff ENCUTGW.
The line HF+E_corr(extrapolated) contains the total energy with the extrapolated value for the RPA correlation energy.
Singles contribution to the correlation energy
The low-scaling RPA algorithm also allows for the determination of the so-called singles contribution,[4][5] to the total energy represented by following diagrams:
In most textbooks[6] this contribution is assumed to be zero. Ren et al.[5] pointed out that this is true only in the Hartree-Fock basis set. The singles contribution is non-vanishing for other basis sets.
The singles contribution is calculated for LSINGLES=.TRUE.. In this case following additional lines can be found in OUTCAR:
HF single shot energy change -1.23182672 renormalized HF singles -1.23310555
Here, the first line contains the value of the singles as proposed by Klimeš et al.,[4] while the second line contains the singles contribution of Ren et al.[5]. In most cases we found that the two values are exceedingly close to each other, which can be understood in the way how the propagator is renormalized.[4]
Optional: RPA Forces
Optionally, RPA forces can be calculated by adding following line to the INCAR file:
LRPAFORCE = .TRUE.
For RPA forces the change in the one-electron density is required.[7] This is automatically performed with the linear-response routine within VASP. After a successful run, the following block of data is found in the OUTCAR file.
POSITION TOTAL RPA FORCE (eV/Angst)
-----------------------------------------------------------------------------------
0.17542 -0.22348 0.17542 -0.292069 7.581315 -0.292069
1.12850 1.31044 1.12850 0.304683 -7.605527 0.304683
-----------------------------------------------------------------------------------
total drift: 0.012614 -0.024212 0.012614
SUGGESTED UPDATED POSCAR (direct coordinates) step
-----------------------------------------------------------------------------------
-0.00958461 -0.00958461 0.13485779 0.04179056 0.04179056 0.00283088
0.25787833 0.25787833 0.22191754 -0.04337198 -0.04337198 0.00431513
The suggested updated positions are also written to the CONTCAR file (if NSW=0). The updated positions are obtained by multiplying the RPA-forces with the parameter DAMP_NEWTON and the inverse of the DFT-Hessian (which is also calculated during the RPA force calculations) and adding the resultant vector to the current positions. DAMP_NEWTON currently defaults to 0.8, but the user might want to change this to 1.0 (no damping), or smaller values if instabilities are observed. The CONTCAR file can be copied to the POSCAR file, and a few such RPA calculations should recover the groundstate structure. Alternatively, standard relaxations (IBRION =1-4) or even MD's can be performed.
Caveats: Noise in Energies and RPA Forces
Generally, the energy calculated by the RPA can be quite noisy as a function of the ionic positions, in particular, if PRECFOCK = FAST and NMAXFOCKAE = 1 is set (these are the default values for RPA calculations). Most of the noise is related to the exact exchange energy. To determine if noise is affecting the results, it is useful to calculate the exchange energy separately as explained in step 2 above. If the exchange energy reported there is smooth, and the exchange energy reported by the all-in-one approach is noisy (e.g. shows odd jumps as a function of the positions or volume), it is strongly recommended to consider one or both of the options discussed below.
Currently, to reduce the noise in the energy and forces, it is sensible to set PRECFOCK = Normal (typically doubling the execution time and memory requirement). It is also possible to set LMAXFOCKAE = -1 (which implicitly sets NMAXFOCKAE = 0). This makes the correlation energies and the related forces less noisy, but technically less accurate (i.e. part of the correlation energy will be missing at high transition energies). Overall, RPA forces must be used carefully and only after extensive testing of all relevant parameters.
Memory bottleneck and Parallelization
The cubic scaling space-time RPA algorithm requires considerably more memory than the corresponding quartic-scaling implementations, two Green's functions have to be stored in real-space. To reduce the memory overhead, VASP exploits Fast Fourier Transformations (FFT) to avoid storage of the matrices on the (larger) real space grid, on the one hand. The precision of the FFT can be selected with PRECFOCK, where usually the values Fast sufficient.
On the other hand, the code avoids storage of redundant information, i.e., both the Green's function and polarizability matrices are distributed as well as the individual imaginary grid points. The distribution of the imaginary grid points can be set by hand with the NTAUPAR and NOMEGAPAR tags, which splits the imaginary grid points NOMEGA into NTAUPAR time and NOMEGAPAR groups. For this purpose both tags have to be divisors of NOMEGA.
The default values are usually reasonable choices provided the tag MAXMEM is set correctly and we strongly recommend to set MAXMEM instead of NTAUPAR.
| Important: As of version 6.2, MAXMEM is estimated automatically (if not set) from the "MemAvailable" entry of the Linux kernel in "/proc/meminfo". |
The required storage for a low-scaling RPA or GW calculation depends mostly on NTAUPAR, the number of MPI groups that share same imaginary time points. A rough estimate for the required bytes is given by
(NGX*NGY*NGZ)*(NGX_S*NGY_S*NGZ_S) / ( NCPU / NTAUPAR ) * 16
where "NCPU" is the number of MPI ranks used for the job,"NGX,NGY,NGZ" denotes the number of FFT grid points for the exact exchange and "NGX_S,NGY_S,NGZ_S" the number of FFT grid points for the supercell. Note, both grids are written to the OUTCAR file after the lines
FFT grid for exact exchange (Hartree Fock) FFT grid for supercell:
The smaller NTAUPAR is set, the less memory per node the job requires to finish successfully.
The approximate memory requirement is calculated in advance and printed to screen and OUTCAR as follows:
min. memory requirement per mpi rank 1234 MB, per node 9872 MB
Some Issues Particular to ACFDT-RPA Calculations on Metals
For metals, the RPA groundstate energy converges the fastest with respect to k-points, if the exchange (Eq. (12) in reference [8]) and correlation energy are calculated on the same k-point grid, HFRCUT is not set, and the long-wavelength contributions from the polarizability are not considered (see reference [8]).
To evaluate Eq. (12), a correction energy for related to partial occupancies has to be added to the RPA groundstate energy:[8]
.
In vasp.5.4.1, this value is calculated for any HF type calculation (step 2) and can be found in the OUTCAR file after the total energy (in the line starting with exchange ACFDT corr. =).
To neglect the long-wavelength contributions, simply set LOPTICS=.FALSE. in the ALGO=Exact step (third step), and remove the WAVEDER files in the directory.
Possible tests and known issues
Basis set convergence
The expression for the ACFDT-RPA correlation energy written in terms of reciprocal lattice vectors reads:
.
The sum over reciprocal lattice vectors has to be truncated at some , determined by < ENCUTGW, which can be set in the INCAR file. The default value is ENCUT, which experience has taught us not to change. For systematic convergence tests, instead increase ENCUT and repeat steps 1 to 4, but be aware that the "maximum number of plane-waves" changes when ENCUT is increased. Note that it is virtually impossible, to converge absolute correlation energies. Rather concentrate on relative energies (e.g. energy differences between two solids, or between a solid and the constituent atoms).
Since correlation energies converge very slowly with respect to , VASP automatically extrapolates to the infinite basis set limit using a linear regression to the equation: [9][8][10]
.
Furthermore, the Coulomb kernel is smoothly truncated between ENCUTGWSOFT and ENCUTGW using a simple cosine like window function (Hann window function). Alternatively, the basis set extrapolation can be performed by setting LSCK=.TRUE., using the squeezed Coulomb kernel method.[11]
The default for ENCUTGWSOFT is 0.8ENCUTGW (again we do not recommend to change this default).
The integral over is evaluated by means of a highly accurate minimax integration.[12] The number of points is determined by the flag NOMEGA, whereas the energy range of transitions is determined by the band gap and the energy difference between the lowest occupied and highest unoccupied one-electron orbital. VASP determines these values automatically (from vasp.5.4.1 on), and the user should only carefully converge with respect to the number of frequency points NOMEGA. A good choice is usually NOMEGA=12, however, for large gap systems one might obtain eV convergence per atom already using 8 points, whereas for metals up to NOMEGA=24 frequency points are sometimes necessary, in particular, for large unit cells.
Strictly adhere to the steps outlines above. Specifically, be aware that steps two and three require the WAVECAR file generated in step one, whereas step four requires the WAVECAR and WAVEDER file generated in step three (generated by setting LOPTICS=.TRUE.).
Convergence with respect to the number of plane waves can be rather slow, and we recommend to test the calculations carefully. Specifically, the calculations should be performed at the default energy cutoff ENCUT, and at an increased cutoff (ideally the default energy cutoff ). Another issue is that energy volume-curves are sometimes not particularly smooth. In that case, the best strategy is to set
ENCUT = 1.3 times default energy cutoff ENCUTGWSOFT = 0.5 times default energy cutoff
where the default energy cutoff is the usual one (maximum ENMAX in POTCAR files). The frequency integration also needs to be checked carefully, in particular for small gap systems (some symmetry broken atoms) convergence can be rather slow, since the one-electron band gap can be very small, requiring a very small minimum in the frequency integration.
K-point convergence: Spline interpolation
| Mind: ESF_SPLINES is available as of VASP.6.5.0 |
It is possible to use spline interpolation to improve upon k-point integration errors by rewriting the RPA correlation energy as an integral over the electronic structure factor:
If ESF_SPLINES=T is set, the code stores the electronic structure factor on a coarse grid defined by KPOINTS and performs a tricubic spline interpolation towards finer q-grids iteratively. After each iteration the RPA correlation energy is evaluated and compared to the result of previous interpolation. If the difference in energy is smaller than ESF_CONV within ESF_NINTER interpolation steps, the code considers the q-point integration to be converged and reports the result to OUTCAR in the following format
cutoff energy smooth cutoff RPA correlation Hartree contr. to MP2 RPA spline-interp.
-----------------------------------------------------------------------------------------------------
166.667 133.333 -12.9738715106 -19.7255874374 -13.4968000908
158.730 126.984 -12.8840657072 -19.6294580403 -13.4017404001
151.172 120.937 -12.7775593388 -19.5151822998 -13.3005326847
143.973 115.178 -12.6604147404 -19.3892142669 -13.1868498210
137.117 109.694 -12.5530911576 -19.2733151174 -13.0861120393
130.588 104.470 -12.4659186304 -19.1786165194 -12.9778587892
124.369 99.495 -12.3690601643 -19.0725742983 -12.8709666989
118.447 94.758 -12.2461267475 -18.9372318755 -12.7590723870
linear regression
converged value -14.0340307585 -20.8751715586 -14.5828037654
The last column contains the result from the spline interpolation for the selected energy cutoffs reported in the first column.
| Warning: Delete WAVEDER for this method. |
Note that this method is incompatible with k-p perturbation theory, where the largest q-point integration error is added explicitly to the RPA integral. This long-wave contribution is stored in WAVEDER, and VASP assumes you want to add this term if the file is present in the working directory.
Also, the long-wave limit is ill-defined for metallic systems, in contrast to the spline interpolation method.
| Mind: ESF_SPLINES can be used for metals. |
Nevertheless, for insulators, we still recommend using WAVEDER and not set ESF_SPLINES for efficiency reasons.
Related Tags and Sections
- ALGO for response functions and ACFDT calculations
- NOMEGA, NOMEGAR number of frequency points
- LHFCALC, switches on HF calculations
- LOPTICS, required in the DFT step to store head and wings
- ENCUTGW, to set cutoff for response functions
- ENCUTGWSOFT
- PRECFOCK controls the FFT grids in HF, GW, RPA calculations
- NTAUPAR controls the number of imaginary time groups in space-time GW and RPA calculations
- NOMEGAPAR controls the number of imaginary frequency groups in space-time GW and RPA calculations
- MAXMEM sets the available memory per MPI rank on each node
- LFINITE_TEMPERATURE switches on Matsubara (finite temperature) formalism
- ESF_SPLINES uses tricubic spline interpolation of electronic structure factor to accelerate k-point convergence
References
- ↑ J. Paier, M. Marsman, and G. Kresse, Phys. Rev. B 78, 121201 (2008).
- ↑ M. Kaltak, J. Klimeš, and G. Kresse, Phys. Rev. B 90, 054115 (2014).
- ↑ H. N. Rojas, R. W. Godby, and R. J. Needs, Phys. Rev. Lett. 74, 1827 (1995).
- ↑ a b c J. Klimeš, M. Kaltak, and G. Kresse, J. Chem. Phys. 143, 102816 (2015).
- ↑ a b c X. Ren, P. Rinke, G. E. Scuseria, and M. Scheffler, Phys. Rev. B 88, 035120 (2013).
- ↑ R. D. Mattuck, Dover Books on Physics (2012).
- ↑ B. Ramberger, T. Schäfer and G. Kresse, Phys. Rev. Lett 118, 106403 (2017).
- ↑ a b c d J. Harl, L. Schimka, and G. Kresse, Phys. Rev. B 81, 115126 (2010).
- ↑ J. Harl and G. Kresse, Phys. Rev. B 77, 045136 (2008).
- ↑ J. Klimeš, M. Kaltak, and G. Kresse, Phys. Rev. B 90, 075125 (2014).
- ↑ S. Riemelmoser, M. Kaltak, and G. Kresse, JCP 152(13), 134103 (2020).
- ↑ M. Kaltak, J. Klimeš, and G. Kresse, J. Chem. Theory Comput. 10, 2498-2507 (2014).