Category:Transition states

From VASP Wiki
Revision as of 12:55, 5 November 2024 by Csheldon (talk | contribs) (→‎Intrinsic reaction coordinate)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Reaction profile for the substitution reaction of chloromethane by chloride. This is a symmetric reaction, where the products and reactants are identical. The maximum of the reaction profile is the transition state (TS). The arrows indicate the direction of motion, showing the attack of the chloromethane by one chloride and then the ejection by the new chloride.

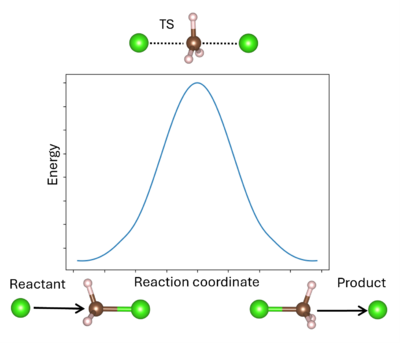
A transition state (TS) in chemistry refers to a high-energy, short-lived configuration that occurs during a chemical reaction as reactants transform into products[1]. At this point, the reaction's progress is maximized. In other words, the transition state is a metastable structure that corresponds to a saddle point on the high-dimensional potential energy surface (PES)[2].

Identifying the transition state is essential for understanding reaction mechanisms, energy barriers, and rates of reaction. The energy barrier is calculated from the energy difference between the reactant R and TS (for the forward reaction) or the product P and TS (for the reverse reaction). It is important to remember that the TS can be reached from either R or P; whichever is more favored depends only on the respective reaction barrier. A single unstable vibrational mode (an imaginary frequency) connects R and P. For comparison to experimental values, additional thermodynamic corrections can be made to the simple energetic barrier, including the zero-point vibrational energy, the population of the vibrational states, and entropy to enable better comparison to the experiment[3]. It is also possible to model solid-solid phase transitions in a similar manner[4].

There are many thorough review articles and books on transition state theory (TST)[5][6] and its subsequent development variational TST (VTST)[7] which we refer to for the interested reader. There are various methods available to pinpoint transition states in VASP.

Static methods

There are three static methods implemented in VASP for finding transition states (TS) using the static, or harmonic, approach: the improved dimer method (IDM), nudged elastic band (NEB), and following the intrinsic reaction coordinate (IRC). IDM takes a guess structure for the TS and then relaxes it along a trial unstable vibrational mode to a first-order saddle point, i.e. the TS. NEB takes the reactant and product structures and interpolates structures between the two to model the reaction pathway. IRC starts at the TS and follows the TS' unstable vibrational mode to reactant and product.

Improved dimer method

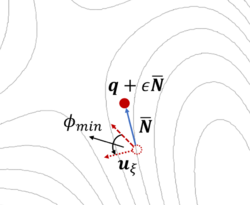
A dimer consisting of two points on the potential energy surface (PES) is rotated to find the lowest curvature. The structure is updated and then a new dimer is defined. The IDM converges towards the desired saddle point, i.e. the TS.

The dimer method[8] is a technique for determining activated transitions without knowledge of the final state. Beginning with a trial transition state (TS) structure, a relaxed TS is obtained. In VASP, the improved dimer method (IDM) by Heyden et al. is implemented. The modification reduces the number of gradient calculations per cycle, improving algorithm performance. A detailed presentation of the method can be found in their paper[9]. The main tag is IBRION=44.

Follow the how-to in order to learn how to perform an IDM calculation.

Nudged elastic bands

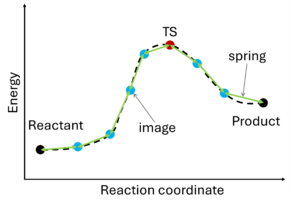
The potential energy surface (PES) is described by a series of images (blue) connected by springs (green arrows). The initial (reactant) and final (product) states are shown in black and remain fixed. The TS is the maximum of the PES (red).

The nudged elastic band (NEB) method[10][11] involves the creation of an initial path connecting the system's initial and final states, utilizing a set of intermediate configurations (IMAGES). Hence, as a prerequisite, the initial and final state (e.g., reactant and product) must be known. The images are interconnected by springs (SPRING), forming a flexible band. Through iterative adjustments (nudging), the positions of the images along the band are modified, minimizing energy until a minimum energy pathway, referred to as the nudged elastic band, is attained.

Learn how to perform an NEB calculation.

Intrinsic reaction coordinate

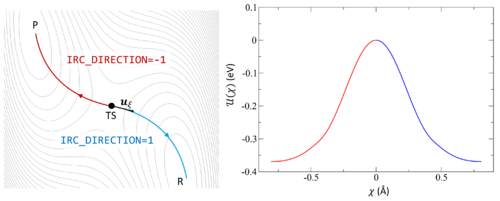
The potential energy surface (PES) is shown as a contour plot. The IRC begins at TS and follows the associated imaginary frequency forward to the product P (red) or backward to the reactant R (blue). The energy is plotted against the complex coordinate to illustrate the energy change as the PES is explored.

Following the intrinsic reaction coordinate (IRC) implies following the steepest descent path from the transition state to reactants and products. The IRC method employs a classical trajectory integration method with fixed velocity, i.e., the damped-velocity Verlet algorithm, incorporating an adaptive time step such that the dynamic reaction pathway resembles the IRC. Hence, as a prerequisite, the transition state must be known. The main tag is IBRION=40.

Learn how to perform an IRC calculation.

Dynamic methods

An alternative to the static approach for modeling the TS, is to use a dynamic (or anharmonic) approach, that is to use molecular dynamics (MD). The static approach models a single structure for the reactant R, TS, and product P. An MD simulation treats each of these states as an ensemble, a combination of many possible structures.

It is difficult using MD to find uncommon states or rare events, such as the TS. An MD simulation is for a short period of time, typically only femto or picoseconds, while seconds would be required to encounter a TS. However, using constrained MD, e.g. a blue moon simulation[12], or metadynamics[13][14], finding even rare events like the TS becomes feasible. More detail for each of these methods, as well as other advanced MD approaches can be found on the relevant advanced MD page.

References

  1. ↑ Transition state theory, www.wikipedia.org (2024)
  2. ↑ H. Hratchian, H. Schlegel, Theory and Application of Computational Chemistry, Chapter 10 - Finding minima, transition states, and following reaction pathways on ab initio potential energy surfaces (2005), p. 195-249
  3. ↑ D. McQuarrie, Statistical Mechanics, (2000).
  4. ↑ D. Sheppard, P. Xiao, W. Chemelweski, D. Johnson, G. Henkelman, A generalized solid-state nudged elastic band method, J. Chem. Phys. 136, 074103 (2012).
  5. ↑ D. Truhlar, B. Garrett, and S. Klippenstein, Current Status of Transition-State Theory, J. Phys. Chem. 100, 12771 (1996).
  6. ↑ M. Roussel, Foundations of Chemical Kinetics, Chapter 7 - Transition-state theory, (2023), p. 195-249.
  7. ↑ J. Bao and D. Truhlar, Variational transition state theory: theoretical framework and recent developments, Chem. Soc. Rev. 46, 7548 (2017).
  8. ↑ G. Henkelman and H. Jónsson, A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives, J. Chem. Phys. 111, 7010–7022 (1999).
  9. ↑ A. Heyden, A. T. Bell, and F. J. Keil, Efficient methods for finding transition states in chemical reactions: Comparison of improved dimer method and partitioned rational function optimization method, J. Chem. Phys. 123, 224101 (2005).
  10. ↑ G. Mills, H. Jonsson and G. K. Schenter, Reversible work transition state theory: application to dissociative adsorption of hydrogen, Surf. Sci., 324, 305 (1995).
  11. ↑ H. Jonsson, G. Mills and K. W. Jacobsen, Nudged Elastic Band Method for Finding Minimum Energy Paths of Transitions, in Classical and Quantum Dynamics in Condensed Phase Simulations, ed. B. J. Berne, G. Ciccotti and D. F. Coker (World Scientific, 1998).
  12. ↑ M. Gešvandtnerová, D. Rocca, T. Bučko, Methanol carbonylation over acid mordenite: Insights from ab initio molecular dynamics and machine learning thermodynamic perturbation theory, J. Catal. 396, 166 (2021).
  13. ↑ B. Ensing, M. De Vivo, Z. Liu, P. Moore, M. Klein, Metadynamics as a Tool for Exploring Free Energy Landscapes of Chemical Reactions, Acc. Chem. Res. 39, 73 (2006)
  14. ↑ P. Tiwary, M. Parrinello, From Metadynamics to Dynamics, Phys. Rev. Lett. 111, 230602 (2013).
Retrieved from "https://www.vasp.at/wiki/index.php?title=Category:Transition_states&oldid=27376"