Charge sloshing
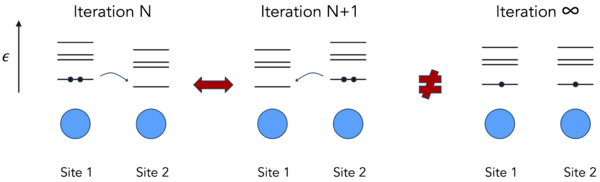
A very handwaving illustration of the phenomenon of charge sloshing during the electronic optimization is shown in Fig. 1:
- Suppose we have a system with two chemically identical sites (Site 1 and 2), and suppose that in step N of the electronic optimization the situation is as follows:
- At the beginning of iteration N, Site 1 is occupied by 2 electrons, Site 2 is empty. After the refinement of the one-electron orbitals, however, the lowest eigenstate associated with Site 2 lies below the occupied state at Site 1.
- In step N+1 the situation is reversed: the two electrons that were on Site 1 now are on Site 2, and after the refinement of the one-electron orbitals the lowest lying state at Site 1 will lie below the occupied state at Site 2.
- In subsequent steps the situation will bounce back-and-forth between the two aforementioned states, without ever reaching the "groundstate" depicted on the right in Fig. 1, where both Site 1 as well as Site 2 are occupied by a single electron.
A bit more mathematical explanation for the occurrence of charge sloshing goes as follows:
- Consider a metal, with "free electron"-like states at the Fermi-level, and consider a very large supercell, in which a single k-point suffices to sample the Brillouin zone, and hence all states are folded back to this point in the Brillouin zone.
- The state just below the Fermi-level is approximately given by , and the one above the Fermi-level by . The former is occupied and the latter is not.
- During the electronic optimization, orbitals and will hybridize. This happens because the gradient of the total energy with respect to the orbitals has a so-called subspace rotational component:
- where are the partial occupancies, and
- is the Hamiltonian expressed within the subspace spanned by the current orbitals .
- A suitable search direction along the subspace rotational part of the gradient is given by a small unitary rotation between orbitals and :
- where denotes the stepsize.
- The aformentioned change in the orbitals leads to a long-wavelength change in the charge density:
- and the consequent change in the Hartree potential due to this long-wavelength change in the density is given by:
- The factor in the above is in fact the principal origin of charge sloshing: a long-wavelength change in the charge density leads to a strongly amplified change in the electrostatic potential.
- In our example, the smallest possible is proportional to L, the maximum extent of the supercell:
- ,
- and thus the response in the potential increases with L2, the square of the maximum extent of the supercell.
- Consequently, the maximum stable step size in a direct optimization algorithm decreases inversely proportional to the square of the maximum extent of the supercell ().
The reasoning above elucidates two important aspects of charge sloshing:
- Metals and systems with a small gap are more prone to charge sloshing than wide-gap insulators.
- Problems due to charge sloshing increase with increasing (super)cell size.
To prevent charge sloshing VASP uses density mixing in the self-consistency cycle.
