Structure optimization

Overview

Structure optimization describes the task of finding the lattice vectors and atom positions that minimize the energy of the system. In its most general form, this optimization problem is extremely challenging because there are usually many local minima. Therefore, we typically limit ourselves to the simpler problem of finding the closest local minimum for a given starting structure. As user, this limitation has two important consequences: (i) You need to make sure that the starting structure is close enough too a minimum for the optimizers to work. (ii) You may need to consider a diverse set of starting structures, if you are not sure about the most reasonable one.

Common considerations

Figure 1: Heuristics for choosing a suitable structure optimization algorithm.

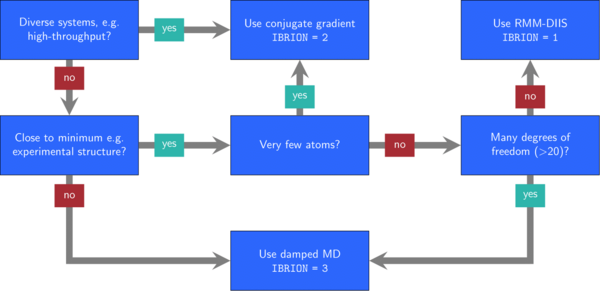
Typically, optimization problems are more difficult to solve, the more free parameters they have. In VASP, you can control the degrees of freedom in different ways: First, use ISIF to determine whether the position of the ions, the shape of the cell, and the volume of the cell change. Second, set selective dynamics in the POSCAR file to decide which ion positions may change.

Next, you need to decide on an algorithm by setting the IBRION tag. In the figure 1, we show some heuristic rules that may help to decide with this selection. These guidelines are a compromise between speed and robustness of the algorithms. The RMM-DIIS algorithm (IBRION = 1) is very efficient because it uses the history of many steps to obtain the best next guess. However, if your structure is still far from the minimum, it is not wise too include the information from these points far from the minimum and the algorithm struggles. The conjugate-gradient (CG) algorithm (IBRION = 2) chooses a search direction conjugate to previous ones. Then it selects an optimal step size along this search direction. This algorithm is a good default choice because of its robustness. Even simpler are damped molcular dynamics (IBRION = 3). This algorithm propagates through time using the forces and friction on the velocities.

All relaxation algorithms (IBRION=1, 2, and 3) rely on a step size POTIM. This step size has no direct physical meaning but scales the forces internally before calling the minimization routine. For many systems, the optimal POTIM is around 0.5. Since the RMM-DIIS algorithm and the damped molecular dynamics are sensitive this parameter, use the conjugate gradient algorithm (IBRION=2), if you are not sure how large the optimal POTIM is.

In this case, the OUTCAR file and stdout will contain a line indicating a reliable POTIM. For IBRION = 2, the following lines will be written to stdout after each corrector step (usually each odd step):

 trial: gam=  .00000 g(F)=   .152E+01 g(S)=  .000E+00 ort = .000E+00
 (trialstep = .82)

The quantity trialstep is the size of the current trialstep. Multiply the current value of POTIM with this number to obtain the optimal step size.

RMM-DIIS

For IBRION = 1, VASP uses a RMM-DIIS algorithm to relax the ions into their instantaneous groundstate. RMM-DIIS stands for residual-minimization method, direct inversion of the iterative subspace. The forces and the stress tensor determine the search directions for finding the equilibrium positions; the total energy is not taken into account. This algorithm is very fast and efficient close to a local minimum, but fails badly if the initial positions are a bad guess (use conjugate gradient instead).

RMM-DIIS implicitly calculates an approximation of the inverse Hessian matrix by taking into account information from previous iterations. The approximation of the Hessian matrix requires very accurate forces, otherwise the algorithm will fail to converge. Enforcing a minimum of electronic steps between each ionic step (NELMIN) converges forces efficiently. For simple bulk materials NELMIN is usually adequate, whereas complex surfaces, where the charge density converges very slowly, might require NELMIN.

On startup, the initial Hessian matrix is diagonal and equal to POTIM. In each iteration a new vector is added to the history. The length of the history determines the rank of the Hessian and must not exceed the degrees of freedom. Naively, one has three degrees of freedom for every ion and nine for the unit cell, but translational invariance, symmetry arguments and constraints can reduce this number significantly. If old steps lead to linear dependencies, they will be automatically removed from the iteration history. When further fine tuning is desired, you can set the NFREE tag to adjust the size of the history.

A reasonable POTIM can speed up calculations significantly. We recommend to find an optimal POTIM using IBRION or performing a few test calculations (see above).

Understanding the output

RMM-DIIS will produce output similar to the following to stdout

BRION: g(F)=  0.463E-01 g(S)=  0.000E+00 retain N=  2 mean eig= 5.94
eig:   5.940  5.940

and the OUTCAR file

 Quasi-Newton relaxation of ions (Broydens 2nd method)                                                                                                                                                                                       
g(Force)  = 0.463E-01   g(Stress)= 0.000E+00
 
 retain information from N=  2 steps
 eigenvalues of (default step * inverse Hessian matrix)
  average eigenvalue of G=   5.9397
 eigenvalue spectrum of G is  5.9397  5.9397

The g values correspond to the norm of the forces and the stress, respectively. VASP also reports the eigenvalues of the approximate Hessian and how many vectors are currently stored in the iteration history.

Conjugate gradient

In the conjugate-gradient algorithm IBRION = 2, we optimize the structure along a search direction. The initial search direction is given by forces and stress; in subsequent steps, we require that the search is conjugate (perpendicular) to the previous direction. Once the search direction is chosen, a line search along this direction determines the optimal step size. Numerical Recipes, by Press et al. contains more details about conjugate gradient.

In VASP, the line search along the search direction uses the following steps

1. We perform a trial step into the search direction. POTIM controls the length of the trial step.
2. We recompute the energy, forces, and stress.
3. Based on the initial energy, the energy after the trial step, and the change of the forces, we fit a cubic or quadratic polynomial to determine the expected minimum (corrector step).
4. We recompute the energy, forces, and stress.
5. If after the corrector step the forces and stress parallel to the current search direction vanish, we perform the next trial step. Otherwise, we improve the line minimization by further corrector steps using a variant of Brent's algorithm.

Tip: If your structure is well suited for the conjugate-gradient algorithm, you should see one initial calculation for the structure in the POSCAR file. Then, VASP should alternate between trial and corrector step.

Understanding the output

In a trial step, you will see similar output like this in the stdout

trial-energy change:   -0.415121  1 .order   -0.385587   -0.435540   -0.335634
step:   3.5233(harm=  3.8400)  dis= 0.29442  next Energy=  -133.730354 (dE=-0.949E+00)

and the OUTCAR file

Conjugate gradient step on ions:
trial-energy change:   -0.415121  1 .order   -0.385587   -0.435540   -0.335634
 (g-gl).g = 0.511E+00      g.g   = 0.494E+00  gl.gl    = 0.245E+01
g(Force)  = 0.494E+00   g(Stress)= 0.000E+00 ortho     = 0.728E-03
gamma     =   0.20820
trial     =   0.88083
opt step  =   3.52334  (harmonic =   3.84000) maximal distance =0.29442102
next E    =  -133.730354   (d E  =  -0.94937)

Of particular interest are the current errors g(Force) and g(Stress), the step size (here 0.88083) in units of POTIM, and the largest distance any ion moves (here 0.29442). You can also compare the expected energy (next E or next Energy) with the energy you obtain in the corrector step.

The other values have the following meaning:

• The trial-energy change is the change of the energy in the trial step
• The values after 1 .order describe the expected energy change resulting from the inner product of gradient and change of the structure. The three different values use the average gradient, the gradient of the previous, and the gradient of the current step, respectively.
• The values step and opt step are the step size of a cubic interpolation; harm and harmonic uses a quadratic interpolation. Close to the minimum these values should agree.
• dE is the expected energy change.

In the corrector step, you will get only output to stdout

curvature:  -0.78 expect dE=-0.387E+00 dE for cont linesearch -0.104E-06
trial: gam= 0.20820 g(F)=  0.494E+00 g(S)=  0.000E+00 ort = 0.728E-03 (trialstep = 0.881E+00)
search vector abs. value=  0.667E+00

You can look at the norm of the forces g(F) and the stress g(S). The ort value tests whether the forces and stress are orthonormal to the previous search direction (should be small). As mentioned above, trialstep is the step size in units of POTIM.

Occasionally, you may get output from ZBRENT. This indicates that the error in the corrector step was too large and the line search is further refined.

Damped molecular dynamics

With IBRION = 3 and SMASS, VASP will execute a damped second order equation of motion for the degrees of freedom

${\ddot {\vec x}} = -2 \alpha {\vec F} - \mu {\dot {\vec x}},$

where SMASS supplies the damping factor μ and POTIM controls α. Discretising the differential equation with a simple velocity Verlet algorithm yields

$\begin{align} {\vec v_{N+1/2}} =& \frac{(2-\mu) {\vec v_{N-1/2}} - 4\alpha {\vec F_N}} {2+\mu}\\ {\vec x_{N+1}} =& {\vec x_{N}} + {\vec v_{N+1/2}} \end{align}$

One may immediately recognize, that μ=2 is equivalent to a simple steepest descent algorithm without line optimization. Hence, μ=2 corresponds to maximal damping, μ=0 corresponds to no damping. The optimal damping factor depends on the second derivatives of the energy with respect to the degrees of freedom. A reasonable first guess for μ is usually 0.4.

Mind that our implementation is particularly user-friendly, since changing μ usually does not require to re-adjust the time step POTIM. To choose an optimal time step and damping factor, we recommend the following two step procedure:

1. Fix μ (for instance to 1) and adjust POTIM. POTIM should be chosen as large as possible without getting divergence in the total energy.
2. Decrease μ and keep POTIM fixed.

If POTIM and SMASS are chosen correctly, the damped molecular dynamics mode may outperform the conjugate gradient method by a factor of two.

If SMASS < 0 a velocity quench algorithm is used.

$\vec v_{\rm quench} = \rm{max}((\vec v + \alpha \vec F) \cdot \vec F, 0) \frac{\vec F}{F^2} + \alpha \vec F$

You can see that velocities are projected onto the forces and only remain if that projection is a positive number.

Mind: For IBRION = 3, a reasonable time step POTIM must be supplied. Too large time steps will result in divergence, too small ones will slow down the convergence. A good choice is usually twice the smallest step size you would observe with the conjugate gradient algorithm.

Understanding the output

The quantity gam is the conjugation parameter to the previous step, g(F) and g(S) are the norm of the force respectively the norm of the stress tensor. The quantity ort is an indicator whether this search direction is orthogonal to the last search direction (for an optimal step this quantity should be much smaller than (g(F) + g(S)). The quantity trialstep is the size of the current trialstep. This value is the average step size leading to a line minimization in the previous ionic step. An optimal POTIM can be determined, by multiplying the current POTIM with the quantity trialstep.

After at the end of a trial step, the following lines are written to stdout:

 trial-energy change:   -1.153185  1.order   -1.133   -1.527  -.739
 step:   1.7275(harm=  2.0557)  dis=  .12277  
                            next Energy= -1341.57 (dE= -.142E+01)

The quantity trial-energy change is the change of the energy in the trial step. The first value after 1.order is the expected energy change calculated from the forces: (F(start)+F(trial))/2×change of positions. The second and third value corresponds to F(start)×change of positions, and F(trial)×change of positions.

The first value in the second line is the size of the step leading to a line minimization along the current search direction. It is calculated from a third order interpolation formula using data from the start and trial step (forces and energy change). harm is the optimal step using a second order (or harmonic) interpolation. Only information on the forces is used for the harmonic interpolation. Close to the minimum both values should be similar. dis is the maximum distance moved by the ions in fractional (direct) coordinates. next Energy gives an indication how large the next energy should be (i.e. the energy at the minimum of the line minimization), dE is the estimated energy change.

The OUTCAR file will contain the following lines, at the end of each trial step:

 trial-energy change:   -1.148928  1.order   -1.126  -1.518  -.735
  (g-gl).g =  .152E+01      g.g   =  .152E+01  gl.gl    =  .000E+00
 g(Force)  =  .152E+01   g(Stress)=  .000E+00 ortho     =  .000E+00
 gamma     =    .00000
 opt step  =   1.72745  (harmonic =   2.05575) max dist = .12277085
 next E    = -1341.577507   (d E  =   1.42496)

The line trial-energy change was already discussed. g(Force) corresponds to g(F), g(Stress) to g(S), ortho to ort, gamma to gam. The values after gamma correspond to the second line (step: ...) previously described.