Self-consistency cycle

The term "Self-Consistency Cycle" (SCC) denotes a category of algorithms that determine the electronic ground state by a combination of iterative matrix diagonalisation and density mixing.

1. The SCC starts with an initial guess for the electronic density of the system under consideration: VASP uses the approximation of overlapping atomic charge densities. This density defines the initial Hamiltonian. The orbitals are initialised with random numbers.
2. By means of iterative matrix diagonalisation techniques one obtains the N lowest lying eigenstates of the Hamiltonian (where N is of the order of the number of electrons in the unit cell). The iterative matrix diagonalisation algorithms implemented in VASP are the blocked-Davidson algorithm and the Residual Minimization Method with Direct Inversion in the Iterative Subspace (RMM-DIIS). Per default VASP uses the blocked-Davidson algorithm (ALGO = Normal).
3. After the eigenstates and eigenvalues have been the determined with sufficient accuracy, they are used to to compute the total energy of the system, and to construct a new electronic density.
4. In principle, this new density could be taken to define a new Hamiltonian. However, in order to arrive at a stable algorithm this new density is not used as is, but is mixed with the old density. By default VASP uses a Broyden mixer. The resulting density then defines the new Hamiltonian for the next round of iterative metrix diagonalisation (step 2).

Steps 2-4 are repeated until the change in the total energy from one cycle to the next drops below a specific threshold (EDIFF).

Note that when starting from scratch (ISTART = 0), the self-consistency cycle procedure of VASP always begins with several (NELMDL) cycles where the density is kept fixed at the initial approximation (overlapping atomic charge densities). This ensures that the wave functions that are initialised with random numbers have converged to a something sensible before they are used to construct a new charge density.

---

The following section discusses the minimization algorithms implemented in VASP. We generally have one outer loop in which the charge density is optimized, and one inner loop in which the wavefunctions are optimized.

Fig. 1:Electronic minimization flowchart

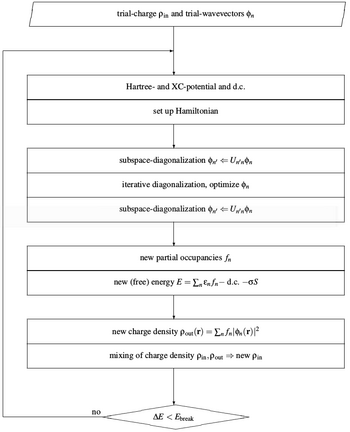
Most of the algorithms implemented in VASP use an iterative matrix-diagonalization scheme, where the used algorithms are based on the conjugate gradient scheme , block Davidson scheme , or a residual minimization scheme -- direct inversion in the iterative subspace (RMM-DIIS) . For the mixing of the charge density an efficient Broyden/Pulay mixing scheme is used. Fig. 1 shows a typical flow-chart of VASP. Input charge density and wavefunctions are independent quantities (at start-up these quantities are set according to INIWAV and ICHARG). Within each selfconsistency loop, the charge density is used to set up the Hamiltonian, then the wavefunctions are optimized iteratively so that they get closer to the exact wavefunctions of this Hamiltonian. From the optimized wavefunctions, a new charge density is calculated, which is then mixed with the old input-charge density.

The conjugate gradient and the residual minimization scheme do not recalculate the exact Kohn-Sham eigenfunctions but an arbitrary linear combination of the NBANDS lowest eigenfunctions. Therefore it is in addition necessary to diagonalize the Hamiltonian in the subspace spanned by the trial-wavefunctions, and to transform the wavefunctions accordingly (i.e. perform a unitary transformation of the wavefunctions, so that the Hamiltonian is diagonal in the subspace spanned by transformed wavefunctions). This step is usually called sub-space diagonalization (although a more appropriate name would be, using the Rayleigh-Ritz variational scheme in a subspace spanned by the wavefunctions):

$\langle \phi_j \ \vert {\bf H} \vert \phi_i \rangle = {\rm H}_{ij},$

$H_{ij} U_{jk} = \epsilon_k U_{ik},$

$\phi_j \leftarrow U_{jk} \phi_k.$

The sub-space diagonalization can be performed before or after the conjugate gradient or residual minimization scheme. Tests we have done indicate that the first choice is preferable during self-consistent calculations.

In general, all iterative algorithms work very similarly. The core quantity is the residual vector

$| R_n \rangle = ({\bf H} - E) | \phi_n \rangle \quad \mbox{with} \quad E = \frac{\langle \phi_n | {\bf H} | \phi_n \rangle}{ \langle \phi_n | \phi_n \rangle }.$

This residual vector is added to the wavefunction $\phi_n$, the algorithms differ in the way this is exactly done.

---