Liquid Si - Freezing: Difference between revisions

From VASP Wiki
VisualWikitext
 
(50 intermediate revisions by 2 users not shown)
Line 2: Line 2:
== Task ==
== Task ==


In this example the goal is to simulate the freezing of liquid Si.
In this example, the goal is to simulate the freezing of liquid Si.


== Input ==
== Input ==
Line 63: Line 63:
   0.6686412136025504  0.7848666926903073  0.5681234351534038
   0.6686412136025504  0.7848666926903073  0.5681234351534038


=== Script for {{TAG|INCAR}} ===
=== {{TAG|INCAR}} ===
{{TAGBL|SYSTEM}} =  Si
# electronic degrees                                                           
{{TAGBL|LREAL}} = A                      # real space projection
{{TAGBL|PREC}}  = Normal                # chose Low only after tests
{{TAGBL|EDIFF}} = 1E-5                  # do not use default (too large drift)
{{TAGBL|ISMEAR}} = -1 ; SIGMA = 0.130    # Fermi smearing: 1500 K 0.086 10-3
{{TAGBL|ALGO}} = Very Fast              # recommended for MD (fall back ALGO = Fast)
{{TAGBL|MAXMIX}} = 40                    # reuse mixer from one MD step to next
{{TAGBL|ISYM}} = 0                      # no symmetry                                   
{{TAGBL|NELMIN}} = 4                    # minimum 4 steps per time step, avoid breaking after 2 steps
# MD (do little writing to save disc space)
{{TAGBL|IBRION}} = 0                    # main molecular dynamics tag
{{TAGBL|NSW}} = 400                      # number of MD steps
{{TAGBL|POTIM}} = 3                      # time step of MD
{{TAGBL|NWRITE}} = 0                    # controls output
{{TAGBL|NBLOCK}} = 10                    # after ten steps pair correlation function is written out
{{TAGBL|LCHARG}} = .FALSE.              # no charge density written out
{{TAGBL|LWAVE}} = .FALSE.                # no wave function coefficients written out
{{TAGBL|TEBEG}} = $i                    # starting temperature for MD
{{TAGBL|TEEND}} = $i                    # end temperature for MD
# canonic (Nose) MD with {{TAGBL|XDATCAR}} updated every 10 steps
{{TAGBL|MDALGO}} = 2                    ä switch to select thermostat
{{TAGBL|SMASS}} =  3                    # Nose mass
{{TAGBL|ISIF}} = 2                      # this tag selects the ensemble in combination with the thermostat
*Most of the tags here are very similar to the tags used in the previous example ({{TAG|Liquid Si - Standard MD}}).
*A stepwise cooling will be applied in this example via a script where $i for {{TAG|TEBEG}} and {{TAG|TEEND}} will be replaced in each calculation (see below).
 
=== {{TAG|KPOINTS}} ===
<pre>
Si-freezing
0 0 0
Gamma
1 1 1
0 0 0
</pre>
*A single k-point is sufficient in this example.
 
== Calculation ==
We will execute the cooling stepwise so several calculations at different temperatures are required in this calculation. The {{TAG|INCAR}} is created with a script for each temperature and run separately. After each step the important files are saved to file.$i, where $i are the temperatures ranging from 2000 to 800 K in steps of 100 K. The script running the calculations looks like the following:
  for i in 2000 1900 1800 1700 1600 1500 1400 1300 1200 1100 1000 900 800
  for i in 2000 1900 1800 1700 1600 1500 1400 1300 1200 1100 1000 900 800
  do
  do
Line 77: Line 116:
  {{TAGBL|ISYM}} = 0                      # no symmetry                                     
  {{TAGBL|ISYM}} = 0                      # no symmetry                                     
  {{TAGBL|NELMIN}} = 4                    # minimum 4 steps per time step, avoid breaking after 2 steps
  {{TAGBL|NELMIN}} = 4                    # minimum 4 steps per time step, avoid breaking after 2 steps
   
  # MD (do little writing to save disc space)
  # MD (do little writing to save disc space)
  {{TAGBL|IBRION}} = 0 ; {{TAGBL|NSW}} = 400 ; {{TAGBL|NWRITE}} = 0 ; {{TAGBL|LCHARG}} = .FALSE. ; {{TAGBL|LWAVE}} = .FALSE.
  {{TAGBL|IBRION}} = 0                     # main molecular dynamics tag
  {{TAGBL|TEBEG}} = $i ; {{TAGBL|TEEND}} = $i
{{TAGBL|NSW}} = 400                     # number of MD steps
{{TAGBL|POTIM}} = 3                      # time step of MD
{{TAGBL|NWRITE}} = 0                     # controls output
{{TAGBL|NBLOCK}} = 10                    # after ten steps pair correlation function is written out
{{TAGBL|LCHARG}} = .FALSE.               # no charge density written out
{{TAGBL|LWAVE}} = .FALSE.               # no wave function coefficients written out
  {{TAGBL|TEBEG}} = $i                     # starting temperature for MD
{{TAGBL|TEEND}} = $i                     # end temperature for MD
  # canonic (Nose) MD with {{TAGBL|XDATCAR}} updated every 10 steps
  # canonic (Nose) MD with {{TAGBL|XDATCAR}} updated every 10 steps
  {{TAGBL|SMASS}} = 3 ; {{TAGBL|NBLOCK}} = 10 ; {{TAGBL|POTIM}} = 3
  {{TAGBL|MDALGO}} = 2                    ä switch to select thermostat
  {{TAGBL|SMASS}} = 3                    # Nose mass
{{TAGBL|ISIF}} = 2                      # this tag selects the ensemble in combination with the thermostat
  !
  !
  mpirun -np 2 /path/to/your/vasp/executable
  mpirun -np 2 /path/to/your/vasp/executable
Line 93: Line 140:
  cp {{TAGBL|CONTCAR}} POSCAR
  cp {{TAGBL|CONTCAR}} POSCAR
  done
  done
*Before running the script one has to replace "'/path/to/your/vasp/executable'" by the path to his "'vasp_gam'" executable. The script is then simply starte by typing the following command in the command line:
bash ./script
=== Diffusion ===
The diffusion coefficient in 3 dimensions is given as
<math> D=\frac{\langle x^{2} \rangle} {6 t}</math>
where t defines time and <math>\langle x^{2} \rangle</math>. The 6 in the denominator contains a factor of 3 accounting for the 3 spatial dimensions (usually the diffusion coefficient is written with a 2 in the denominator in literature corresponding to only one dimension). In our case, we calculate the above equation as follows


<tt>script</tt> performs molecular dynamics runs on liquid Si at decreasing temperatures, starting at 2000 K and ending at 800 K. This should contain the transition from liquid Si to crystalline Si (amorphous).
<math> D=\frac{\langle \sum_{i}^{N}  [x_{i}(t)-x_{i}(0)]^{2} \rangle}{6 \Delta t} </math>.


=== {{TAG|KPOINTS}} ===
Here the diffusion coefficient is calculated over an ensemble average to get better statistics.  Our calculations were carried out for 1200 fs for each temperature. We will average in our case over the last 900 fs regarding the first 300 fs as equilibration of each temperature. The following python script (''diffusion_coefficient.py'') calculates the diffusion coefficient at a given temperature:
 
<div class="toccolours mw-customtoggle-script">'''Click to show/''diffusion_coefficient.py''</div>
<div class="mw-collapsible mw-collapsed" id="mw-customcollapsible-script">
<pre>
<pre>
test
#!/usr/bin/python
0 0 0
 
monk
import sys
1 1 1
import re
0 0 0
import math
 
#setting grid for histogram
 
potim = 3                              #timestep from INCAR file
readfile = open(sys.argv[1],"r")        #input XDATCAR file in format XDATCAR.TEMP
temp=re.sub("XDATCAR.",,sys.argv[1])  #extracts temperature from input file name
z=0                                     #counter
natoms=0                               #number of atoms in XDATCAR file
posion = []                            #atom positions in Cartesian coordinates
confcount = 0                           #number of structures in XDATCAR file
direct=[]                              #number of time steps for each structure in XDATCAR file
a=[]                                    #lattice parameter in 1st dimension
b=[]                                    #lattice parameter in 2nd dimension
c=[]                                    #lattice parameter in 3rd dimension
#read in XDATCAR file
line=readfile.readline()
while (line):
  z=z+1
  line.strip()
  line=re.sub('^',' ',line)
  y=line.split()
  if (z==2):
    scale=float(y[0])
  if (z==3):
    a.append(float(y[0]))
    a.append(float(y[1]))
    a.append(float(y[2]))
    a_len=(a[0]*a[0]+a[1]*a[1]+a[2]*a[2])**0.5
  if (z==4):
    b.append(float(y[0]))
    b.append(float(y[1]))
    b.append(float(y[2]))
    b_len=(b[0]*b[0]+b[1]*b[1]+b[2]*b[2])**0.5
  if (z==5):
    c.append(float(y[0]))
    c.append(float(y[1]))
    c.append(float(y[2]))
    c_len=(c[0]*c[0]+c[1]*c[1]+c[2]*c[2])**0.5
  if (z==7):
    natoms=int(y[0])
  if (y[0]=="Direct"):
    direct.append(int(y[2]))
    posion.append([])
    for i in range(0,natoms):
        line=readfile.readline()
        line.strip()
        line=re.sub('^',' ',line)
        f=line.split()
        cartpos_x=a[0]*float(f[0])+a[1]*float(f[1])+a[2]*float(f[2])
        cartpos_y=b[0]*float(f[0])+b[1]*float(f[1])+b[2]*float(f[2])
        cartpos_z=c[0]*float(f[0])+c[1]*float(f[1])+c[2]*float(f[2])
        #positions of ions for each structure are obtained here
        posion[confcount].append([cartpos_x,cartpos_y,cartpos_z])
    confcount=confcount+1
  line=readfile.readline()
readfile.close
 
#calculate diffusion coefficient
#skip first 10 configurations corresponding to 300 fs
d=0.0
for i in range(10,confcount):
  for j in range(0,natoms):
      x_diff=posion[i][j][0]-posion[0][j][0]
      #if length is larger than 0.5 (in crystallographic coordinates) then we have to shift atom
      #due to periodic image to obtain the shortest distance.
      if (abs(x_diff)>(0.5*a_len)):
        if (x_diff<0):
            x_diff=x_diff+a_len
        elif (x_diff>0):
            x_diff=x_diff-a_len
      y_diff=posion[i][j][1]-posion[0][j][1]
      if (abs(y_diff)>(0.5*b_len)):
        if (y_diff<0):
            y_diff=y_diff+b_len
        elif (y_diff>0):
            y_diff=y_diff-b_len
      z_diff=posion[i][j][2]-posion[0][j][2]
      if (abs(z_diff)>(0.5*c_len)):
        if (z_diff<0):
            z_diff=z_diff+c_len
        elif (x_diff>0):
            z_diff=z_diff-c_len
      d=d+x_diff**2.0+y_diff**2.0+z_diff**2.0  
 
#print diffusion coefficient (in Ang^2/ps) vs temperature (in K)
d=d/(confcount-1-10)/natoms/6.0
time=(direct[confcount-1]-direct[10])*potim/10**3.0 #conversion to ps
print temp,d/time
</pre>
</pre>
</div>
Since the atoms can move such that the distance between old and new positions becomes larger than 0.5 (in crystallographic or fractional coordinates). Let us take for example the movement of atom 0 in the <math>x</math> direction from 0 to -0.25, which would be output in the {{TAG|CONTCAR}} as 0.75. The distance corresponding to that would be then calculated as 0.75 which is wrong since we have periodic images and the real shortest distance would be 0.25. Hence all distances larger than 0.5 have to be shifted by -1.0. This is taken care of in the script.
We will use a short bash script (''dscript.sh'') to calculate the diffusion coefficient at different temperatures and plot them in a file (diff_coeff.jpg):
#!/bin/bash
if test -f "diff_coeff.dat"; then
    rm diff_coeff.dat
fi
touch diff_coeff.dat
for i in 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000; do
    diffusion_coefficient.py XDATCAR.$i >>  diff_coeff.dat
done
gnuplot -e "set terminal jpeg; set key left; set xlabel 'temperature (K)'; set ylabel 'D (Ang^2/ps)'; set style data lines; plot 'diff_coeff.dat' " > diff_coeff.jpg
To execute it just type the following command:
bash ./dscript.sh
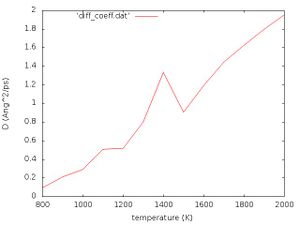
The data for the diffusion coefficient at each temperature is output to ''diff_coeff.dat'' and plotted in ''diff_coeff.jpg'' which should look like the following:
[[File:Diff coeff.jpg|300px|]]


'''Exercise''': Interpret Fig. 1 yourself!


== Calculation ==
<div class="toccolours mw-customtoggle-script2">'''Click to show/Solution'''</div>
<div class="mw-collapsible mw-collapsed" id="mw-customcollapsible-script2">'''Solution''':
For a given phase the diffusion coefficient depends directly on the temperature by
 
<math> D=\mu k_{B} T</math>
 
where <math>k_{B}</math> is the Boltzmann constant and <math>\mu</math> is the mobility of the particle. Evidently, this relation is approximately fulfilled in Fig. 1. At approximately 1400 K we see a peak. This temperature should correspond to the phase transition temperature.
Close to the phase transition point the scaling with respect to the reduced temperature <math>T_{\mathrm{red}}</math> becomes
 
<math> \langle x^{2} \rangle \propto T_{\mathrm{red}}^{1-\alpha},\qquad \qquad \qquad T_{\mathrm{red}}=\frac{T-T_{c}}{T_{c}}</math>


*To analyse the diffusion behaviour at a certain temperature T, the data read from {{TAG|XDATCAR.T}} can be processed
where <math> \alpha </math> is an anomalous dimension (it may be positive or negative) and <math>T_{c}</math> is the critical temperature. For infinite large systems and infinite time, this would lead to a singularity in the plot, but since we are dealing with a finite-sized system it results in a finite peak at the phase transition point.
using the script diffusion ('''caution - this script is written for VASP version 4.x output'''):
</div>


<pre>
=== Pair correlation function ===
awk <XDATCAR  >diffusion.xy '
#
# simple module function
#
function mod(x,y) { return x-int(x/y)*y }
function minim(x) { return mod(x+2.5,1.0)-0.5 }
#
# calculate mean square displacement
#
function diff() {
      d=0
      for (ion=1; ion<=ions; ion++) {
        dx=minim(xn[ion]-x[ion])
        dy=minim(yn[ion]-y[ion])
        dz=minim(zn[ion]-z[ion])


        xn[ion]=x[ion]+dx
The pair-correlation function provides information about the probability of finding two atoms at a given distance <math> r </math>.
        yn[ion]=y[ion]+dy
The pair-correlation function is save for each temperature under  ''PCDAT.T''. The following script will plot the pair correlation functions at different temperatures in one figure:
        zn[ion]=z[ion]+dz
#!/bin/bash
for i in 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000; do
    awk <PCDAT.$i >pair.$i ' NR==8 {pcskal=$1} NR==9 {pcfein=$1} NR>=10036 {line=line+1; print (line-0.5)*pcfein/pcskal,$1} '
done
gnuplot -e "set terminal jpeg; set key left; set xlabel 'r (Ang)'; set ylabel 'PCF'; set style data lines; plot 'pair.2000','pair.1400','pair.800' " > pair.jpg
To execute it type the following command:
bash ./pair.sh


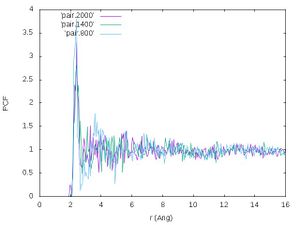
The plot should look like the following:


        d=d+(xn[ion]-x0[ion])*(xn[ion]-x0[ion])*a1*a1
[[File:Pair liquid Si freezing.jpg|300px]]
        d=d+(yn[ion]-y0[ion])*(yn[ion]-y0[ion])*a2*a2
        d=d+(zn[ion]-z0[ion])*(zn[ion]-z0[ion])*a3*a3
      }
#      d=d/(set*t)/6
        d=d/6
        print set*t,d
}
#
# set the number of ions
#
NR==1 { ions = $1 }
NR==2 { a1=$2*10^10 ;  a2=$3*10^10 ;  a3=$4*10^10 ; t=$5*10^12 }
#
# at this point a complete set of ionic positions has been found
#
mod(NR-6,ions+1)==0 {
    if (set>=2) diff()
    if (set==1) {
      for (ion=1; ion<=ions; ion++) {
        x0[ion]=xn[ion]
        y0[ion]=yn[ion]
        z0[ion]=zn[ion]
      }
    }
    for (ion=1; ion<=ions; ion++) {
        x[ion]=xn[ion]
        y[ion]=yn[ion]
        z[ion]=zn[ion]
    }
    head=headn
    headn=$0
    set=set+1
}
# store coordinates
mod(NR-6,ions+1)>0  {
    ion=mod(NR-6,ions+1)
    xn[ion]=$1
    yn[ion]=$2
    zn[ion]=$3
}
'
</pre>


*The pair-correlation function written on {{FILE|PCDAT.[T]}} should be processed using the script PCDATtoPCDATxy:
'''Exercise:''' Interpret the figure yourself!


<pre>
<div class="toccolours mw-customtoggle-script3">'''Click to show/Solution'''</div>
awk <PCDAT >PCDAT.xy '
<div class="mw-collapsible mw-collapsed" id="mw-customcollapsible-script3">'''Solution''':
NR==8 { pcskal=$1}
Crystalline structures usually have less diffuse pair correlation functions since the atoms are usually vibrating around high symmetry points. In liquids, the average positions are smeared out over a wider range of distances. With decreasing temperature, the pair correlation function in the plot gets more structured. This indicates that crystallization is happening.
NR==9 { pcfein=$1}
</div>
NR>=13 {
  line=line+1
  if (line==257)  {
    print " "
    line=0
  }
  else
    print (line-0.5)*pcfein/pcskal,$1
}
'
</pre>


'''Mind''': You will have to set the correct path to your VASP executable and invoke VASP with the correct command (e.g., in the above: <tt>mpirun -np 2</tt>).


== Download ==
== Download ==
[http://www.vasp.at/vasp-workshop/examples/Si_liquid.tgz Si_liquid.tgz]
[[Media:Si_Liquid_Freezing.tgz| Si_Liquid_Freezing.tgz]]
   
   
{{Template:Bulk_systems}}
{{Template:Molecular dynamics - Tutorial}}


[[Category:Examples]]
[[Category:Examples]]

Latest revision as of 15:00, 15 April 2022

Task

In this example, the goal is to simulate the freezing of liquid Si.

Input

POSCAR

Si
15.12409564534287297131
     0.5000000000000000    0.5000000000000000    0.0000000000000000
     0.0000000000000000    0.5000000000000000    0.5000000000000000
     0.5000000000000000    0.0000000000000000    0.5000000000000000
  48
Direct
  0.8550657259653851  0.3204575801875221  0.6180363868822553
  0.6045454476433229  0.0546379652195404  0.1629680405553871
  0.4803889256776521  0.2999635319377835  0.0131251454718051
  0.8413504226620471  0.7598095803296524  0.1917781560970181
  0.9754163118144437  0.6134171268457649  0.7421364242876367
  0.2668229391055025  0.0066502741664650  0.0031140604380929
  0.8935777664000575  0.3324172908647429  0.9535738516718881
  0.0527608886321274  0.5249316429131962  0.5293744880144071
  0.4396089233132741  0.7564833235979471  0.5665855438788387
  0.5907859878830199  0.5198033580597228  0.3581725847640679
  0.2120832721474721  0.4042899613004446  0.7921535013319151
  0.0225803885096466  0.8414911198321031  0.1209255489569852
  0.0992500701525566  0.3917384466892963  0.3612433325214984
  0.9673794138223195  0.5206425706394114  0.1719623236201897
  0.2774602656926126  0.8480860088162007  0.2673309412777037
  0.0196991774214161  0.8282178425383616  0.6986213756952502
  0.3570927152895376  0.2951488295546784  0.2651851032568589
  0.1663829731894614  0.9766237917413699  0.6051764245375237
  0.4931841331696695  0.8689890620771937  0.2612357008392290
  0.8006473407426477  0.1033419073227807  0.4706563716777467
  0.0161340851939779  0.9953827418297991  0.8853439845676159
  0.7827740166661069  0.1821830067208054  0.9399555168314748
  0.0720651739141343  0.2539424963694544  0.6857919074323433
  0.4443385370769313  0.0486404637002326  0.4180706114402839
  0.7055263679666055  0.6802623819082319  0.7983614866719116
  0.2237125282521105  0.4055474352416297  0.0077044950891134
  0.2963682069847125  0.5771265542042112  0.2019757061665083
  0.2782449529809642  0.0451513130915826  0.7644934848784113
  0.9312079203181675  0.9090938018377080  0.3429249881187518
  0.6341882597200124  0.2969253226419481  0.3227590981305088
  0.3587691103780569  0.1061057273904179  0.0931868777500710
  0.8710437838676732  0.6541301230631744  0.4261617089364881
  0.6784300588817769  0.3263889355408940  0.5560491395978739
  0.5597052314845080  0.0174390112509929  0.6129003207931863
  0.0595962318875451  0.1019295953521402  0.3340999072062676
  0.7689671766774326  0.1768870209149794  0.1604177484299765
  0.9603661624482890  0.3311649224573259  0.1439224909303592
  0.3792868784787023  0.2806150985211180  0.4921541531665999
  0.8079860889823454  0.9194188799048340  0.9131036494263627
  0.3002081239026374  0.7834053620019006  0.8650323716139056
  0.4704528574512951  0.7221628305989689  0.9746107190983403
  0.2886552568292480  0.5927625600330780  0.4239421203107919
  0.4116743942942291  0.2198943758058664  0.7072597030225044
  0.2104494234814825  0.6457654201409418  0.8275863924787099
  0.6784628197745537  0.7205455185203838  0.1093053357228383
  0.6344130299021448  0.1650970001101275  0.8037018707797643
  0.3965793440603315  0.5364088146415013  0.6064549771969059
  0.6686412136025504  0.7848666926903073  0.5681234351534038

INCAR

SYSTEM =  Si
# electronic degrees                                                            
LREAL = A                      # real space projection
PREC  = Normal                 # chose Low only after tests
EDIFF = 1E-5                   # do not use default (too large drift)
ISMEAR = -1 ; SIGMA = 0.130    # Fermi smearing: 1500 K 0.086 10-3
ALGO = Very Fast               # recommended for MD (fall back ALGO = Fast)
MAXMIX = 40                    # reuse mixer from one MD step to next
ISYM = 0                       # no symmetry                                    
NELMIN = 4                     # minimum 4 steps per time step, avoid breaking after 2 steps
# MD (do little writing to save disc space)
IBRION = 0                     # main molecular dynamics tag
NSW = 400                      # number of MD steps
POTIM = 3                      # time step of MD
NWRITE = 0                     # controls output
NBLOCK = 10                    # after ten steps pair correlation function is written out
LCHARG = .FALSE.               # no charge density written out
LWAVE = .FALSE.                # no wave function coefficients written out
TEBEG = $i                     # starting temperature for MD
TEEND = $i                     # end temperature for MD
# canonic (Nose) MD with XDATCAR updated every 10 steps
MDALGO = 2                     ä switch to select thermostat
SMASS =  3                     # Nose mass
ISIF = 2                       # this tag selects the ensemble in combination with the thermostat
  • Most of the tags here are very similar to the tags used in the previous example (Liquid Si - Standard MD).
  • A stepwise cooling will be applied in this example via a script where $i for TEBEG and TEEND will be replaced in each calculation (see below).

KPOINTS

Si-freezing
0 0 0
Gamma
 1 1 1
 0 0 0
  • A single k-point is sufficient in this example.

Calculation

We will execute the cooling stepwise so several calculations at different temperatures are required in this calculation. The INCAR is created with a script for each temperature and run separately. After each step the important files are saved to file.$i, where $i are the temperatures ranging from 2000 to 800 K in steps of 100 K. The script running the calculations looks like the following: 

for i in 2000 1900 1800 1700 1600 1500 1400 1300 1200 1100 1000 900 800
do
cat >INCAR <<!
SYSTEM =  Si
# electronic degrees                                                            
LREAL = A                      # real space projection
PREC  = Normal                 # chose Low only after tests
EDIFF = 1E-5                   # do not use default (too large drift)
ISMEAR = -1 ; SIGMA = 0.130    # Fermi smearing: 1500 K 0.086 10-3
ALGO = Very Fast               # recommended for MD (fall back ALGO = Fast)
MAXMIX = 40                    # reuse mixer from one MD step to next
ISYM = 0                       # no symmetry                                    
NELMIN = 4                     # minimum 4 steps per time step, avoid breaking after 2 steps
# MD (do little writing to save disc space)
IBRION = 0                     # main molecular dynamics tag
NSW = 400                      # number of MD steps
POTIM = 3                      # time step of MD
NWRITE = 0                     # controls output
NBLOCK = 10                    # after ten steps pair correlation function is written out
LCHARG = .FALSE.               # no charge density written out
LWAVE = .FALSE.                # no wave function coefficients written out
TEBEG = $i                     # starting temperature for MD
TEEND = $i                     # end temperature for MD
# canonic (Nose) MD with XDATCAR updated every 10 steps
MDALGO = 2                     ä switch to select thermostat
SMASS =  3                     # Nose mass
ISIF = 2                       # this tag selects the ensemble in combination with the thermostat
!
mpirun -np 2 /path/to/your/vasp/executable
cp XDATCAR XDATCAR.$i
cp OUTCAR OUTCAR.$i
cp PCDAT PCDAT.$i
cp CONTCAR CONTCAR.$i
cp POSCAR POSCAR.$i
cp OSZICAR OSZICAR.$i
cp CONTCAR POSCAR
done
  • Before running the script one has to replace "'/path/to/your/vasp/executable'" by the path to his "'vasp_gam'" executable. The script is then simply starte by typing the following command in the command line:
bash ./script

Diffusion

The diffusion coefficient in 3 dimensions is given as

where t defines time and . The 6 in the denominator contains a factor of 3 accounting for the 3 spatial dimensions (usually the diffusion coefficient is written with a 2 in the denominator in literature corresponding to only one dimension). In our case, we calculate the above equation as follows

.

Here the diffusion coefficient is calculated over an ensemble average to get better statistics. Our calculations were carried out for 1200 fs for each temperature. We will average in our case over the last 900 fs regarding the first 300 fs as equilibration of each temperature. The following python script (diffusion_coefficient.py) calculates the diffusion coefficient at a given temperature:

Click to show/diffusion_coefficient.py
#!/usr/bin/python

import sys
import re
import math

#setting grid for histogram

potim = 3                               #timestep from INCAR file
readfile = open(sys.argv[1],"r")        #input XDATCAR file in format XDATCAR.TEMP
temp=re.sub("XDATCAR.",,sys.argv[1])  #extracts temperature from input file name
z=0                                     #counter
natoms=0                                #number of atoms in XDATCAR file
posion = []                             #atom positions in Cartesian coordinates
confcount = 0                           #number of structures in XDATCAR file
direct=[]                               #number of time steps for each structure in XDATCAR file
a=[]                                    #lattice parameter in 1st dimension
b=[]                                    #lattice parameter in 2nd dimension
c=[]                                    #lattice parameter in 3rd dimension
#read in XDATCAR file
line=readfile.readline()
while (line):
  z=z+1
  line.strip()
  line=re.sub('^',' ',line)
  y=line.split()
  if (z==2):
     scale=float(y[0])
  if (z==3):
     a.append(float(y[0]))
     a.append(float(y[1]))
     a.append(float(y[2]))
     a_len=(a[0]*a[0]+a[1]*a[1]+a[2]*a[2])**0.5
  if (z==4):
     b.append(float(y[0]))
     b.append(float(y[1]))
     b.append(float(y[2]))
     b_len=(b[0]*b[0]+b[1]*b[1]+b[2]*b[2])**0.5
  if (z==5):
     c.append(float(y[0]))
     c.append(float(y[1]))
     c.append(float(y[2]))
     c_len=(c[0]*c[0]+c[1]*c[1]+c[2]*c[2])**0.5
  if (z==7):
     natoms=int(y[0])
  if (y[0]=="Direct"):
     direct.append(int(y[2]))
     posion.append([])
     for i in range(0,natoms):
        line=readfile.readline()
        line.strip()
        line=re.sub('^',' ',line)
        f=line.split()
        cartpos_x=a[0]*float(f[0])+a[1]*float(f[1])+a[2]*float(f[2])
        cartpos_y=b[0]*float(f[0])+b[1]*float(f[1])+b[2]*float(f[2])
        cartpos_z=c[0]*float(f[0])+c[1]*float(f[1])+c[2]*float(f[2])
        #positions of ions for each structure are obtained here
        posion[confcount].append([cartpos_x,cartpos_y,cartpos_z])
     confcount=confcount+1
  line=readfile.readline()
readfile.close

#calculate diffusion coefficient
#skip first 10 configurations corresponding to 300 fs
d=0.0
for i in range(10,confcount):
   for j in range(0,natoms):
      x_diff=posion[i][j][0]-posion[0][j][0]
      #if length is larger than 0.5 (in crystallographic coordinates) then we have to shift atom
      #due to periodic image to obtain the shortest distance.
      if (abs(x_diff)>(0.5*a_len)):
         if (x_diff<0):
            x_diff=x_diff+a_len
         elif (x_diff>0):
            x_diff=x_diff-a_len
      y_diff=posion[i][j][1]-posion[0][j][1]
      if (abs(y_diff)>(0.5*b_len)):
         if (y_diff<0):
            y_diff=y_diff+b_len
         elif (y_diff>0):
            y_diff=y_diff-b_len
      z_diff=posion[i][j][2]-posion[0][j][2]
      if (abs(z_diff)>(0.5*c_len)):
         if (z_diff<0):
            z_diff=z_diff+c_len
         elif (x_diff>0):
            z_diff=z_diff-c_len
      d=d+x_diff**2.0+y_diff**2.0+z_diff**2.0 

#print diffusion coefficient (in Ang^2/ps) vs temperature (in K)
d=d/(confcount-1-10)/natoms/6.0
time=(direct[confcount-1]-direct[10])*potim/10**3.0 #conversion to ps
print temp,d/time


Since the atoms can move such that the distance between old and new positions becomes larger than 0.5 (in crystallographic or fractional coordinates). Let us take for example the movement of atom 0 in the direction from 0 to -0.25, which would be output in the CONTCAR as 0.75. The distance corresponding to that would be then calculated as 0.75 which is wrong since we have periodic images and the real shortest distance would be 0.25. Hence all distances larger than 0.5 have to be shifted by -1.0. This is taken care of in the script.

We will use a short bash script (dscript.sh) to calculate the diffusion coefficient at different temperatures and plot them in a file (diff_coeff.jpg): 

#!/bin/bash

if test -f "diff_coeff.dat"; then
   rm diff_coeff.dat
fi

touch diff_coeff.dat

for i in 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000; do
   diffusion_coefficient.py XDATCAR.$i >>  diff_coeff.dat
done

gnuplot -e "set terminal jpeg; set key left; set xlabel 'temperature (K)'; set ylabel 'D (Ang^2/ps)'; set style data lines; plot 'diff_coeff.dat' " > diff_coeff.jpg


To execute it just type the following command: 

bash ./dscript.sh

The data for the diffusion coefficient at each temperature is output to diff_coeff.dat and plotted in diff_coeff.jpg which should look like the following:

Exercise: Interpret Fig. 1 yourself!

Click to show/Solution
Solution:

For a given phase the diffusion coefficient depends directly on the temperature by

where is the Boltzmann constant and is the mobility of the particle. Evidently, this relation is approximately fulfilled in Fig. 1. At approximately 1400 K we see a peak. This temperature should correspond to the phase transition temperature. Close to the phase transition point the scaling with respect to the reduced temperature becomes

where is an anomalous dimension (it may be positive or negative) and is the critical temperature. For infinite large systems and infinite time, this would lead to a singularity in the plot, but since we are dealing with a finite-sized system it results in a finite peak at the phase transition point.

Pair correlation function

The pair-correlation function provides information about the probability of finding two atoms at a given distance . The pair-correlation function is save for each temperature under PCDAT.T. The following script will plot the pair correlation functions at different temperatures in one figure: 

#!/bin/bash

for i in 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000; do
   awk <PCDAT.$i >pair.$i ' NR==8 {pcskal=$1} NR==9 {pcfein=$1} NR>=10036 {line=line+1; print (line-0.5)*pcfein/pcskal,$1} '
done

gnuplot -e "set terminal jpeg; set key left; set xlabel 'r (Ang)'; set ylabel 'PCF'; set style data lines; plot 'pair.2000','pair.1400','pair.800' " > pair.jpg

To execute it type the following command: 

bash ./pair.sh

The plot should look like the following:

Exercise: Interpret the figure yourself!

Click to show/Solution
Solution:

Crystalline structures usually have less diffuse pair correlation functions since the atoms are usually vibrating around high symmetry points. In liquids, the average positions are smeared out over a wider range of distances. With decreasing temperature, the pair correlation function in the plot gets more structured. This indicates that crystallization is happening.


Download

Si_Liquid_Freezing.tgz

Retrieved from "https://www.vasp.at/wiki/index.php?title=Liquid_Si_-_Freezing&oldid=17487"