Structure optimization: Difference between revisions
m (Schlipf moved page VASP Wiki:Structure optimization to Structure optimization) |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 43: | Line 43: | ||
For {{TAGO|IBRION|1}}, VASP uses a RMM-DIIS algorithm to relax the ions into their instantaneous groundstate. | For {{TAGO|IBRION|1}}, VASP uses a RMM-DIIS algorithm to relax the ions into their instantaneous groundstate. | ||
RMM-DIIS stands for ''residual-minimization method, direct inversion | RMM-DIIS stands for ''residual-minimization method, direct inversion in the iterative subspace''.{{cite|pulay:cpl:1980}} | ||
The forces and the stress tensor determine the search directions for finding the equilibrium positions; the total energy is not taken into account. | The forces and the stress tensor determine the search directions for finding the equilibrium positions; the total energy is not taken into account. | ||
This algorithm is very fast and efficient close to a local minimum, but fails badly if the initial positions are a bad guess (use [[#Conjugate gradient|conjugate gradient]] instead). | This algorithm is very fast and efficient close to a local minimum, but fails badly if the initial positions are a bad guess (use [[#Conjugate gradient|conjugate gradient]] instead). | ||
| Line 180: | Line 180: | ||
In both cases ''g(F)'' and ''g(S)'' are the norm of forces and stress. | In both cases ''g(F)'' and ''g(S)'' are the norm of forces and stress. | ||
The extra line in the latter case is a sanity check on the average velocities and should produce vanishingly small numbers. | The extra line in the latter case is a sanity check on the average velocities and should produce vanishingly small numbers. | ||
== Related tags and articles == | |||
{{TAG|IBRION}}, | |||
{{TAG|POTIM}}, | |||
{{TAG|NSW}}, | |||
{{TAG|SMASS}} | |||
== References == | == References == | ||
<references/> | <references/> | ||
[[Category:Ionic minimization]][[Category:Howto]][[Category:Forces]] | |||
Latest revision as of 11:39, 21 October 2024
Overview
Structure optimization describes the task of finding the lattice vectors and atom positions that minimize the energy of the system. In its most general form, this optimization problem is extremely challenging because there are usually many local minima. Therefore, we typically limit ourselves to the simpler problem of finding the closest local minimum for a given starting structure. As user, this limitation has two important consequences: (i) You need to make sure that the starting structure is close enough to a minimum for the optimizers to work. (ii) You may need to consider a diverse set of starting structures, if you are not sure about the most reasonable one.
Common considerations
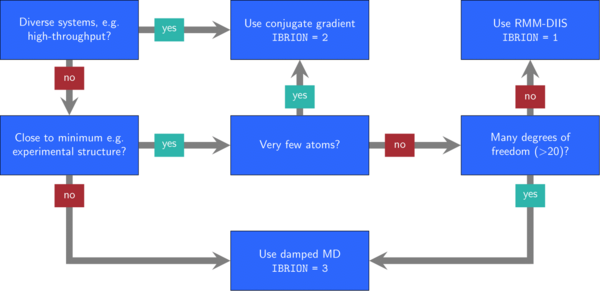
Typically, optimization problems are more difficult to solve, the more free parameters they have. In VASP, you can control the degrees of freedom in different ways: First, use ISIF to determine whether the position of the ions, the shape of the cell, and the volume of the cell change. Second, set selective dynamics in the POSCAR file to decide which ion positions may change.
Next, you need to decide on an algorithm by setting the IBRION tag.
In Figure 1, we show some heuristic rules that may help to decide with this selection.
These guidelines are a compromise between speed and robustness of the algorithms.
The RMM-DIIS algorithm (IBRION = 1) is very efficient because it uses the history of many steps to obtain the best next guess.
However, if your structure is still far from the minimum, it is not wise too include the information from these points far from the minimum and the algorithm struggles.
The conjugate-gradient (CG) algorithm (IBRION = 2) chooses a search direction conjugate to previous ones.
Then it selects an optimal step size along this search direction.
This algorithm is a good default choice because of its robustness.
Even simpler are damped molcular dynamics (IBRION = 3).
This algorithm propagates through time using the forces and friction on the velocities.
All relaxation algorithms (IBRION=1, 2, and 3) rely on a step size POTIM.
This step size has no direct physical meaning but scales the forces internally before calling the minimization routine.
For many systems, the optimal POTIM is around 0.5.
Since the RMM-DIIS algorithm and the damped molecular dynamics are sensitive this parameter, use the conjugate gradient algorithm (IBRION=2), if you are not sure how large the optimal POTIM is.
In this case, the OUTCAR file and stdout will contain a line indicating a reliable POTIM.
For IBRION = 2, the following lines will be written to stdout after each corrector step (usually each odd step):
trial: gam= 0.20820 g(F)= 0.494E+00 g(S)= 0.000E+00 ort = 0.728E-03 (trialstep = 0.881E+00)
The quantity trialstep is the size of the current trialstep. Multiply the current value of POTIM with this number to obtain the optimal step size.
RMM-DIIS
For IBRION = 1, VASP uses a RMM-DIIS algorithm to relax the ions into their instantaneous groundstate.
RMM-DIIS stands for residual-minimization method, direct inversion in the iterative subspace.[1]
The forces and the stress tensor determine the search directions for finding the equilibrium positions; the total energy is not taken into account.
This algorithm is very fast and efficient close to a local minimum, but fails badly if the initial positions are a bad guess (use conjugate gradient instead).
RMM-DIIS implicitly calculates an approximation of the inverse Hessian matrix by taking into account information from previous iterations.
The approximation of the Hessian matrix requires very accurate forces, otherwise the algorithm will fail to converge.
Enforcing a minimum of electronic steps between each ionic step (NELMIN) converges forces efficiently.
For simple bulk materials NELMIN = 4 is usually adequate, whereas complex surfaces, where the charge density converges very slowly, might require NELMIN = 8.
On startup, the initial Hessian matrix is diagonal and equal to POTIM. In each iteration a new vector is added to the history. The length of the history determines the rank of the Hessian and must not exceed the degrees of freedom. Naively, one has three degrees of freedom for every ion and nine for the unit cell, but translational invariance, symmetry arguments and constraints can reduce this number significantly. If old steps lead to linear dependencies, they will be automatically removed from the iteration history. When further fine tuning is desired, you can set the NFREE tag to adjust the size of the history.
A reasonable POTIM can speed up calculations significantly.
We recommend to find an optimal POTIM using IBRION = 2 or performing a few test calculations (see above).
Understanding the output
RMM-DIIS will produce output similar to the following to stdout
BRION: g(F)= 0.463E-01 g(S)= 0.000E+00 retain N= 2 mean eig= 5.94 eig: 5.940 5.940
and the OUTCAR file
Quasi-Newton relaxation of ions (Broydens 2nd method) g(Force) = 0.463E-01 g(Stress)= 0.000E+00 retain information from N= 2 steps eigenvalues of (default step * inverse Hessian matrix) average eigenvalue of G= 5.9397 eigenvalue spectrum of G is 5.9397 5.9397
The g values correspond to the norm of the forces and the stress, respectively. VASP also reports the eigenvalues of the approximate Hessian and how many vectors are currently stored in the iteration history.
Conjugate gradient
In the conjugate-gradient algorithm IBRION = 2, we optimize the structure along a search direction.
The initial search direction is given by forces and stress;
in subsequent steps, we require that the search is conjugate (perpendicular) to the previous direction.
Once the search direction is chosen, a line search along this direction determines the optimal step size.
Numerical Recipes by Press et al. contains more details about conjugate gradient.[2]
In VASP, the line search along the search direction uses the following steps
- We perform a trial step into the search direction. POTIM controls the length of the trial step.
- We recompute the energy, forces, and stress.
- Based on the initial energy, the energy after the trial step, and the change of the forces, we fit a cubic or quadratic polynomial to determine the expected minimum (corrector step).
- We recompute the energy, forces, and stress.
- If after the corrector step the forces and stress parallel to the current search direction vanish, we perform the next trial step. Otherwise, we improve the line minimization by further corrector steps using a variant of Brent's algorithm.[2]
| Tip: If your structure is well suited for the conjugate-gradient algorithm, you should see one initial calculation for the structure in the POSCAR file. Then, VASP should alternate between trial and corrector step. |
Understanding the output
In a trial step, you will see similar output like this in the stdout
trial-energy change: -0.415121 1 .order -0.385587 -0.435540 -0.335634 step: 3.5233(harm= 3.8400) dis= 0.29442 next Energy= -133.730354 (dE=-0.949E+00)
and the OUTCAR file
Conjugate gradient step on ions: trial-energy change: -0.415121 1 .order -0.385587 -0.435540 -0.335634 (g-gl).g = 0.511E+00 g.g = 0.494E+00 gl.gl = 0.245E+01 g(Force) = 0.494E+00 g(Stress)= 0.000E+00 ortho = 0.728E-03 gamma = 0.20820 trial = 0.88083 opt step = 3.52334 (harmonic = 3.84000) maximal distance =0.29442102 next E = -133.730354 (d E = -0.94937)
Of particular interest are the current errors g(Force) and g(Stress), the step size (here 0.88083) in units of POTIM, and the largest distance any ion moves (here 0.29442). You can also compare the expected energy (next E or next Energy) with the energy you obtain in the corrector step.
The other values have the following meaning:
- The trial-energy change is the change of the energy in the trial step
- The values after 1 .order describe the expected energy change resulting from the inner product of gradient and change of the structure. The three different values use the average gradient, the gradient of the previous, and the gradient of the current step, respectively.
- The values step and opt step are the step size of a cubic interpolation; harm and harmonic uses a quadratic interpolation. Close to the minimum these values should agree.
- dE is the expected energy change.
In the corrector step, you will get only output to stdout
curvature: -0.78 expect dE=-0.387E+00 dE for cont linesearch -0.104E-06 trial: gam= 0.20820 g(F)= 0.494E+00 g(S)= 0.000E+00 ort = 0.728E-03 (trialstep = 0.881E+00) search vector abs. value= 0.667E+00
You can look at the norm of the forces g(F) and the stress g(S). The ort value tests whether the forces and stress are orthogonal to the previous search direction (should be small). As mentioned above, trialstep is the step size in units of POTIM.
Occasionally, you may get output from ZBRENT. This indicates that the error in the corrector step was too large and the line search is further refined.
Damped molecular dynamics
With IBRION = 3 and SMASS, VASP will execute a damped second order equation of motion for the degrees of freedom
where SMASS supplies the damping factor μ and POTIM controls α. Discretising the differential equation with a simple velocity Verlet algorithm yields
One may immediately recognize, that μ=2 is equivalent to a simple steepest descent algorithm without line optimization. Hence, μ=2 corresponds to maximal damping, μ=0 corresponds to no damping. The optimal damping factor depends on the second derivatives of the energy with respect to the degrees of freedom. A reasonable first guess for μ is usually 0.4.
Mind that our implementation is particularly user-friendly, since changing μ usually does not require to re-adjust the time step POTIM. To choose an optimal time step and damping factor, we recommend the following two step procedure:
- Fix μ (for instance to 1) and adjust POTIM. POTIM should be chosen as large as possible without getting divergence in the total energy.
- Decrease μ and keep POTIM fixed.
If POTIM and SMASS are chosen correctly, the damped molecular dynamics mode may outperform the conjugate gradient method by a factor of two.
If SMASS < 0 a velocity quench algorithm is used.
You can see that velocities are projected onto the forces and only remain if that projection is a positive number.
Mind: For IBRION = 3, a reasonable time step POTIM must be supplied. Too large time steps will result in divergence, too small ones will slow down the convergence. A good choice is usually twice the smallest step size you would observe with the conjugate gradient algorithm.
|
Understanding the output
Damped molecular dynamics produces relatively little output compared to the other two algorithms. If SMASS is set to a value larger than 0, you will see output like this in stdout
damped: g(F)= 0.159E+01 g(S)= 0.000E+00 dE (1.order)=-0.254E+01
otherwise for the quenched velocity algorithm you get output similar to this
summed vel is now 0.0000000000000000 0.0000000000000000 5.5511151231257827E-017 quench: g(F)= 0.191E+02 g(S)= 0.000E+00 dE (1.order)=-0.311E+02
In both cases g(F) and g(S) are the norm of forces and stress. The extra line in the latter case is a sanity check on the average velocities and should produce vanishingly small numbers.
