Liquid Si - Freezing: Difference between revisions
| (5 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
== Task == | == Task == | ||
In this example the goal is to simulate the freezing of liquid Si. | In this example, the goal is to simulate the freezing of liquid Si. | ||
== Input == | == Input == | ||
| Line 148: | Line 148: | ||
<math> D=\frac{\langle x^{2} \rangle} {6 t}</math> | <math> D=\frac{\langle x^{2} \rangle} {6 t}</math> | ||
where t defines time and <math>\langle x^{2} \rangle</math>. The 6 in the denominator contains a factor of 3 accounting for the 3 spatial dimensions (usually the diffusion coefficient is written with a 2 in the denominator in literature corresponding to only one dimension). In our case we calculate the above equation as follows | where t defines time and <math>\langle x^{2} \rangle</math>. The 6 in the denominator contains a factor of 3 accounting for the 3 spatial dimensions (usually the diffusion coefficient is written with a 2 in the denominator in literature corresponding to only one dimension). In our case, we calculate the above equation as follows | ||
<math> D=\frac{\langle \sum_{i}^{N} [x_{i}(t)-x_{i}(0)]^{2} \rangle}{6 \Delta t} </math>. | <math> D=\frac{\langle \sum_{i}^{N} [x_{i}(t)-x_{i}(0)]^{2} \rangle}{6 \Delta t} </math>. | ||
| Line 155: | Line 155: | ||
<div class="toccolours mw-customtoggle-script">'''Click to show/''diffusion_coefficient.py''</div> | <div class="toccolours mw-customtoggle-script">'''Click to show/''diffusion_coefficient.py''</div> | ||
<div class="mw-collapsible mw-collapsed" id="mw-customcollapsible-script"> | <div class="mw-collapsible mw-collapsed" id="mw-customcollapsible-script"> | ||
<pre> | |||
#!/usr/bin/python | |||
import sys | |||
import re | |||
import math | |||
#setting grid for histogram | |||
potim = 3 #timestep from INCAR file | |||
readfile = open(sys.argv[1],"r") #input XDATCAR file in format XDATCAR.TEMP | |||
temp=re.sub("XDATCAR.",,sys.argv[1]) #extracts temperature from input file name | |||
z=0 #counter | |||
natoms=0 #number of atoms in XDATCAR file | |||
posion = [] #atom positions in Cartesian coordinates | |||
confcount = 0 #number of structures in XDATCAR file | |||
direct=[] #number of time steps for each structure in XDATCAR file | |||
a=[] #lattice parameter in 1st dimension | |||
b=[] #lattice parameter in 2nd dimension | |||
c=[] #lattice parameter in 3rd dimension | |||
#read in XDATCAR file | |||
line=readfile.readline() | |||
while (line): | |||
z=z+1 | |||
line.strip() | |||
line=re.sub('^',' ',line) | |||
y=line.split() | |||
if (z==2): | |||
scale=float(y[0]) | |||
if (z==3): | |||
a.append(float(y[0])) | |||
a.append(float(y[1])) | |||
a.append(float(y[2])) | |||
a_len=(a[0]*a[0]+a[1]*a[1]+a[2]*a[2])**0.5 | |||
if (z==4): | |||
b.append(float(y[0])) | |||
b.append(float(y[1])) | |||
b.append(float(y[2])) | |||
b_len=(b[0]*b[0]+b[1]*b[1]+b[2]*b[2])**0.5 | |||
if (z==5): | |||
c.append(float(y[0])) | |||
c.append(float(y[1])) | |||
c.append(float(y[2])) | |||
c_len=(c[0]*c[0]+c[1]*c[1]+c[2]*c[2])**0.5 | |||
if (z==7): | |||
natoms=int(y[0]) | |||
if (y[0]=="Direct"): | |||
direct.append(int(y[2])) | |||
posion.append([]) | |||
for i in range(0,natoms): | |||
line=readfile.readline() | |||
line.strip() | |||
line=re.sub('^',' ',line) | |||
f=line.split() | |||
cartpos_x=a[0]*float(f[0])+a[1]*float(f[1])+a[2]*float(f[2]) | |||
cartpos_y=b[0]*float(f[0])+b[1]*float(f[1])+b[2]*float(f[2]) | |||
cartpos_z=c[0]*float(f[0])+c[1]*float(f[1])+c[2]*float(f[2]) | |||
#positions of ions for each structure are obtained here | |||
posion[confcount].append([cartpos_x,cartpos_y,cartpos_z]) | |||
confcount=confcount+1 | |||
line=readfile.readline() | |||
readfile.close | |||
#calculate diffusion coefficient | |||
#skip first 10 configurations corresponding to 300 fs | |||
d=0.0 | |||
for i in range(10,confcount): | |||
for j in range(0,natoms): | |||
x_diff=posion[i][j][0]-posion[0][j][0] | |||
#if length is larger than 0.5 (in crystallographic coordinates) then we have to shift atom | |||
#due to periodic image to obtain the shortest distance. | |||
if (abs(x_diff)>(0.5*a_len)): | |||
if (x_diff<0): | |||
x_diff=x_diff+a_len | |||
elif (x_diff>0): | |||
x_diff=x_diff-a_len | |||
y_diff=posion[i][j][1]-posion[0][j][1] | |||
if (abs(y_diff)>(0.5*b_len)): | |||
if (y_diff<0): | |||
y_diff=y_diff+b_len | |||
elif (y_diff>0): | |||
y_diff=y_diff-b_len | |||
z_diff=posion[i][j][2]-posion[0][j][2] | |||
if (abs(z_diff)>(0.5*c_len)): | |||
if (z_diff<0): | |||
z_diff=z_diff+c_len | |||
elif (x_diff>0): | |||
z_diff=z_diff-c_len | |||
d=d+x_diff**2.0+y_diff**2.0+z_diff**2.0 | |||
Since the atoms can move such that the distance between old and new | #print diffusion coefficient (in Ang^2/ps) vs temperature (in K) | ||
d=d/(confcount-1-10)/natoms/6.0 | |||
time=(direct[confcount-1]-direct[10])*potim/10**3.0 #conversion to ps | |||
print temp,d/time | |||
</pre> | |||
</div> | |||
Since the atoms can move such that the distance between old and new positions becomes larger than 0.5 (in crystallographic or fractional coordinates). Let us take for example the movement of atom 0 in the <math>x</math> direction from 0 to -0.25, which would be output in the {{TAG|CONTCAR}} as 0.75. The distance corresponding to that would be then calculated as 0.75 which is wrong since we have periodic images and the real shortest distance would be 0.25. Hence all distances larger than 0.5 have to be shifted by -1.0. This is taken care of in the script. | |||
We will use a short bash script (''dscript.sh'') to calculate the diffusion coefficient at different temperatures and plot them in a file (diff_coeff.jpg): | We will use a short bash script (''dscript.sh'') to calculate the diffusion coefficient at different temperatures and plot them in a file (diff_coeff.jpg): | ||
| Line 190: | Line 286: | ||
<math> D=\mu k_{B} T</math> | <math> D=\mu k_{B} T</math> | ||
where <math>k_{B}</math> is the Boltzmann constant and <math>\mu</math> is the mobility of the particle. Evidently this relation is approximately fulfilled in Fig. 1. At approximately 1400 K we see a peak. This temperature should correspond to the phase transition temperature. | where <math>k_{B}</math> is the Boltzmann constant and <math>\mu</math> is the mobility of the particle. Evidently, this relation is approximately fulfilled in Fig. 1. At approximately 1400 K we see a peak. This temperature should correspond to the phase transition temperature. | ||
Close to the phase transition point the scaling with respect to the reduced temperature <math>T_{\mathrm{red}}</math> becomes | Close to the phase transition point the scaling with respect to the reduced temperature <math>T_{\mathrm{red}}</math> becomes | ||
<math> \langle x^{2} \rangle \propto T_{\mathrm{red}}^{1-\alpha},\qquad \qquad \qquad T_{\mathrm{red}}=\frac{T-T_{c}}{T_{c}}</math> | <math> \langle x^{2} \rangle \propto T_{\mathrm{red}}^{1-\alpha},\qquad \qquad \qquad T_{\mathrm{red}}=\frac{T-T_{c}}{T_{c}}</math> | ||
where <math> \alpha </math> is an anomalous dimension (it may be positive or negative) and <math>T_{c}</math> is the critical temperature. For infinite large systems and infinite time this would lead to a singularity in the plot, but since we are dealing with a finite sized system it results in a finite peak at the phase transition point. | where <math> \alpha </math> is an anomalous dimension (it may be positive or negative) and <math>T_{c}</math> is the critical temperature. For infinite large systems and infinite time, this would lead to a singularity in the plot, but since we are dealing with a finite-sized system it results in a finite peak at the phase transition point. | ||
</div> | </div> | ||
| Line 216: | Line 312: | ||
[[File:Pair liquid Si freezing.jpg|300px]] | [[File:Pair liquid Si freezing.jpg|300px]] | ||
''' | '''Exercise:''' Interpret the figure yourself! | ||
<div class="toccolours mw-customtoggle-script3">'''Click to show/Solution'''</div> | |||
<div class="mw-collapsible mw-collapsed" id="mw-customcollapsible-script3">'''Solution''': | |||
Crystalline structures usually have less diffuse pair correlation functions since the atoms are usually vibrating around high symmetry points. In liquids, the average positions are smeared out over a wider range of distances. With decreasing temperature, the pair correlation function in the plot gets more structured. This indicates that crystallization is happening. | |||
</div> | |||
== Download == | == Download == | ||
[ | [[Media:Si_Liquid_Freezing.tgz| Si_Liquid_Freezing.tgz]] | ||
{{Template: | {{Template:Molecular dynamics - Tutorial}} | ||
[[Category:Examples]] | [[Category:Examples]] | ||
Latest revision as of 15:00, 15 April 2022
Task
In this example, the goal is to simulate the freezing of liquid Si.
Input
POSCAR
Si
15.12409564534287297131
0.5000000000000000 0.5000000000000000 0.0000000000000000
0.0000000000000000 0.5000000000000000 0.5000000000000000
0.5000000000000000 0.0000000000000000 0.5000000000000000
48
Direct
0.8550657259653851 0.3204575801875221 0.6180363868822553
0.6045454476433229 0.0546379652195404 0.1629680405553871
0.4803889256776521 0.2999635319377835 0.0131251454718051
0.8413504226620471 0.7598095803296524 0.1917781560970181
0.9754163118144437 0.6134171268457649 0.7421364242876367
0.2668229391055025 0.0066502741664650 0.0031140604380929
0.8935777664000575 0.3324172908647429 0.9535738516718881
0.0527608886321274 0.5249316429131962 0.5293744880144071
0.4396089233132741 0.7564833235979471 0.5665855438788387
0.5907859878830199 0.5198033580597228 0.3581725847640679
0.2120832721474721 0.4042899613004446 0.7921535013319151
0.0225803885096466 0.8414911198321031 0.1209255489569852
0.0992500701525566 0.3917384466892963 0.3612433325214984
0.9673794138223195 0.5206425706394114 0.1719623236201897
0.2774602656926126 0.8480860088162007 0.2673309412777037
0.0196991774214161 0.8282178425383616 0.6986213756952502
0.3570927152895376 0.2951488295546784 0.2651851032568589
0.1663829731894614 0.9766237917413699 0.6051764245375237
0.4931841331696695 0.8689890620771937 0.2612357008392290
0.8006473407426477 0.1033419073227807 0.4706563716777467
0.0161340851939779 0.9953827418297991 0.8853439845676159
0.7827740166661069 0.1821830067208054 0.9399555168314748
0.0720651739141343 0.2539424963694544 0.6857919074323433
0.4443385370769313 0.0486404637002326 0.4180706114402839
0.7055263679666055 0.6802623819082319 0.7983614866719116
0.2237125282521105 0.4055474352416297 0.0077044950891134
0.2963682069847125 0.5771265542042112 0.2019757061665083
0.2782449529809642 0.0451513130915826 0.7644934848784113
0.9312079203181675 0.9090938018377080 0.3429249881187518
0.6341882597200124 0.2969253226419481 0.3227590981305088
0.3587691103780569 0.1061057273904179 0.0931868777500710
0.8710437838676732 0.6541301230631744 0.4261617089364881
0.6784300588817769 0.3263889355408940 0.5560491395978739
0.5597052314845080 0.0174390112509929 0.6129003207931863
0.0595962318875451 0.1019295953521402 0.3340999072062676
0.7689671766774326 0.1768870209149794 0.1604177484299765
0.9603661624482890 0.3311649224573259 0.1439224909303592
0.3792868784787023 0.2806150985211180 0.4921541531665999
0.8079860889823454 0.9194188799048340 0.9131036494263627
0.3002081239026374 0.7834053620019006 0.8650323716139056
0.4704528574512951 0.7221628305989689 0.9746107190983403
0.2886552568292480 0.5927625600330780 0.4239421203107919
0.4116743942942291 0.2198943758058664 0.7072597030225044
0.2104494234814825 0.6457654201409418 0.8275863924787099
0.6784628197745537 0.7205455185203838 0.1093053357228383
0.6344130299021448 0.1650970001101275 0.8037018707797643
0.3965793440603315 0.5364088146415013 0.6064549771969059
0.6686412136025504 0.7848666926903073 0.5681234351534038
INCAR
SYSTEM = Si # electronic degrees LREAL = A # real space projection PREC = Normal # chose Low only after tests EDIFF = 1E-5 # do not use default (too large drift) ISMEAR = -1 ; SIGMA = 0.130 # Fermi smearing: 1500 K 0.086 10-3 ALGO = Very Fast # recommended for MD (fall back ALGO = Fast) MAXMIX = 40 # reuse mixer from one MD step to next ISYM = 0 # no symmetry NELMIN = 4 # minimum 4 steps per time step, avoid breaking after 2 steps # MD (do little writing to save disc space) IBRION = 0 # main molecular dynamics tag NSW = 400 # number of MD steps POTIM = 3 # time step of MD NWRITE = 0 # controls output NBLOCK = 10 # after ten steps pair correlation function is written out LCHARG = .FALSE. # no charge density written out LWAVE = .FALSE. # no wave function coefficients written out TEBEG = $i # starting temperature for MD TEEND = $i # end temperature for MD # canonic (Nose) MD with XDATCAR updated every 10 steps MDALGO = 2 ä switch to select thermostat SMASS = 3 # Nose mass ISIF = 2 # this tag selects the ensemble in combination with the thermostat
- Most of the tags here are very similar to the tags used in the previous example (Liquid Si - Standard MD).
- A stepwise cooling will be applied in this example via a script where $i for TEBEG and TEEND will be replaced in each calculation (see below).
KPOINTS
Si-freezing 0 0 0 Gamma 1 1 1 0 0 0
- A single k-point is sufficient in this example.
Calculation
We will execute the cooling stepwise so several calculations at different temperatures are required in this calculation. The INCAR is created with a script for each temperature and run separately. After each step the important files are saved to file.$i, where $i are the temperatures ranging from 2000 to 800 K in steps of 100 K. The script running the calculations looks like the following:
for i in 2000 1900 1800 1700 1600 1500 1400 1300 1200 1100 1000 900 800 do cat >INCAR <<! SYSTEM = Si # electronic degrees LREAL = A # real space projection PREC = Normal # chose Low only after tests EDIFF = 1E-5 # do not use default (too large drift) ISMEAR = -1 ; SIGMA = 0.130 # Fermi smearing: 1500 K 0.086 10-3 ALGO = Very Fast # recommended for MD (fall back ALGO = Fast) MAXMIX = 40 # reuse mixer from one MD step to next ISYM = 0 # no symmetry NELMIN = 4 # minimum 4 steps per time step, avoid breaking after 2 steps # MD (do little writing to save disc space) IBRION = 0 # main molecular dynamics tag NSW = 400 # number of MD steps POTIM = 3 # time step of MD NWRITE = 0 # controls output NBLOCK = 10 # after ten steps pair correlation function is written out LCHARG = .FALSE. # no charge density written out LWAVE = .FALSE. # no wave function coefficients written out TEBEG = $i # starting temperature for MD TEEND = $i # end temperature for MD # canonic (Nose) MD with XDATCAR updated every 10 steps MDALGO = 2 ä switch to select thermostat SMASS = 3 # Nose mass ISIF = 2 # this tag selects the ensemble in combination with the thermostat ! mpirun -np 2 /path/to/your/vasp/executable cp XDATCAR XDATCAR.$i cp OUTCAR OUTCAR.$i cp PCDAT PCDAT.$i cp CONTCAR CONTCAR.$i cp POSCAR POSCAR.$i cp OSZICAR OSZICAR.$i cp CONTCAR POSCAR done
- Before running the script one has to replace "'/path/to/your/vasp/executable'" by the path to his "'vasp_gam'" executable. The script is then simply starte by typing the following command in the command line:
bash ./script
Diffusion
The diffusion coefficient in 3 dimensions is given as
where t defines time and . The 6 in the denominator contains a factor of 3 accounting for the 3 spatial dimensions (usually the diffusion coefficient is written with a 2 in the denominator in literature corresponding to only one dimension). In our case, we calculate the above equation as follows
.
Here the diffusion coefficient is calculated over an ensemble average to get better statistics. Our calculations were carried out for 1200 fs for each temperature. We will average in our case over the last 900 fs regarding the first 300 fs as equilibration of each temperature. The following python script (diffusion_coefficient.py) calculates the diffusion coefficient at a given temperature:
#!/usr/bin/python
import sys
import re
import math
#setting grid for histogram
potim = 3 #timestep from INCAR file
readfile = open(sys.argv[1],"r") #input XDATCAR file in format XDATCAR.TEMP
temp=re.sub("XDATCAR.",,sys.argv[1]) #extracts temperature from input file name
z=0 #counter
natoms=0 #number of atoms in XDATCAR file
posion = [] #atom positions in Cartesian coordinates
confcount = 0 #number of structures in XDATCAR file
direct=[] #number of time steps for each structure in XDATCAR file
a=[] #lattice parameter in 1st dimension
b=[] #lattice parameter in 2nd dimension
c=[] #lattice parameter in 3rd dimension
#read in XDATCAR file
line=readfile.readline()
while (line):
z=z+1
line.strip()
line=re.sub('^',' ',line)
y=line.split()
if (z==2):
scale=float(y[0])
if (z==3):
a.append(float(y[0]))
a.append(float(y[1]))
a.append(float(y[2]))
a_len=(a[0]*a[0]+a[1]*a[1]+a[2]*a[2])**0.5
if (z==4):
b.append(float(y[0]))
b.append(float(y[1]))
b.append(float(y[2]))
b_len=(b[0]*b[0]+b[1]*b[1]+b[2]*b[2])**0.5
if (z==5):
c.append(float(y[0]))
c.append(float(y[1]))
c.append(float(y[2]))
c_len=(c[0]*c[0]+c[1]*c[1]+c[2]*c[2])**0.5
if (z==7):
natoms=int(y[0])
if (y[0]=="Direct"):
direct.append(int(y[2]))
posion.append([])
for i in range(0,natoms):
line=readfile.readline()
line.strip()
line=re.sub('^',' ',line)
f=line.split()
cartpos_x=a[0]*float(f[0])+a[1]*float(f[1])+a[2]*float(f[2])
cartpos_y=b[0]*float(f[0])+b[1]*float(f[1])+b[2]*float(f[2])
cartpos_z=c[0]*float(f[0])+c[1]*float(f[1])+c[2]*float(f[2])
#positions of ions for each structure are obtained here
posion[confcount].append([cartpos_x,cartpos_y,cartpos_z])
confcount=confcount+1
line=readfile.readline()
readfile.close
#calculate diffusion coefficient
#skip first 10 configurations corresponding to 300 fs
d=0.0
for i in range(10,confcount):
for j in range(0,natoms):
x_diff=posion[i][j][0]-posion[0][j][0]
#if length is larger than 0.5 (in crystallographic coordinates) then we have to shift atom
#due to periodic image to obtain the shortest distance.
if (abs(x_diff)>(0.5*a_len)):
if (x_diff<0):
x_diff=x_diff+a_len
elif (x_diff>0):
x_diff=x_diff-a_len
y_diff=posion[i][j][1]-posion[0][j][1]
if (abs(y_diff)>(0.5*b_len)):
if (y_diff<0):
y_diff=y_diff+b_len
elif (y_diff>0):
y_diff=y_diff-b_len
z_diff=posion[i][j][2]-posion[0][j][2]
if (abs(z_diff)>(0.5*c_len)):
if (z_diff<0):
z_diff=z_diff+c_len
elif (x_diff>0):
z_diff=z_diff-c_len
d=d+x_diff**2.0+y_diff**2.0+z_diff**2.0
#print diffusion coefficient (in Ang^2/ps) vs temperature (in K)
d=d/(confcount-1-10)/natoms/6.0
time=(direct[confcount-1]-direct[10])*potim/10**3.0 #conversion to ps
print temp,d/time
Since the atoms can move such that the distance between old and new positions becomes larger than 0.5 (in crystallographic or fractional coordinates). Let us take for example the movement of atom 0 in the direction from 0 to -0.25, which would be output in the CONTCAR as 0.75. The distance corresponding to that would be then calculated as 0.75 which is wrong since we have periodic images and the real shortest distance would be 0.25. Hence all distances larger than 0.5 have to be shifted by -1.0. This is taken care of in the script.
We will use a short bash script (dscript.sh) to calculate the diffusion coefficient at different temperatures and plot them in a file (diff_coeff.jpg):
#!/bin/bash if test -f "diff_coeff.dat"; then rm diff_coeff.dat fi touch diff_coeff.dat for i in 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000; do diffusion_coefficient.py XDATCAR.$i >> diff_coeff.dat done gnuplot -e "set terminal jpeg; set key left; set xlabel 'temperature (K)'; set ylabel 'D (Ang^2/ps)'; set style data lines; plot 'diff_coeff.dat' " > diff_coeff.jpg
To execute it just type the following command:
bash ./dscript.sh
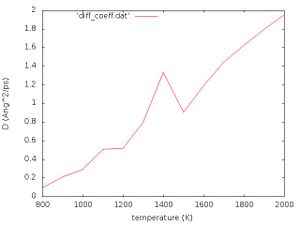
The data for the diffusion coefficient at each temperature is output to diff_coeff.dat and plotted in diff_coeff.jpg which should look like the following:
Exercise: Interpret Fig. 1 yourself!
For a given phase the diffusion coefficient depends directly on the temperature by
where is the Boltzmann constant and is the mobility of the particle. Evidently, this relation is approximately fulfilled in Fig. 1. At approximately 1400 K we see a peak. This temperature should correspond to the phase transition temperature. Close to the phase transition point the scaling with respect to the reduced temperature becomes
where is an anomalous dimension (it may be positive or negative) and is the critical temperature. For infinite large systems and infinite time, this would lead to a singularity in the plot, but since we are dealing with a finite-sized system it results in a finite peak at the phase transition point.
Pair correlation function
The pair-correlation function provides information about the probability of finding two atoms at a given distance . The pair-correlation function is save for each temperature under PCDAT.T. The following script will plot the pair correlation functions at different temperatures in one figure:
#!/bin/bash
for i in 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000; do
awk <PCDAT.$i >pair.$i ' NR==8 {pcskal=$1} NR==9 {pcfein=$1} NR>=10036 {line=line+1; print (line-0.5)*pcfein/pcskal,$1} '
done
gnuplot -e "set terminal jpeg; set key left; set xlabel 'r (Ang)'; set ylabel 'PCF'; set style data lines; plot 'pair.2000','pair.1400','pair.800' " > pair.jpg
To execute it type the following command:
bash ./pair.sh
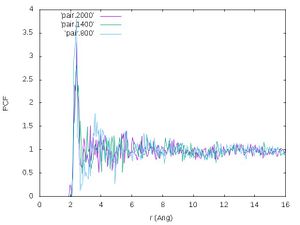
The plot should look like the following:
Exercise: Interpret the figure yourself!
Crystalline structures usually have less diffuse pair correlation functions since the atoms are usually vibrating around high symmetry points. In liquids, the average positions are smeared out over a wider range of distances. With decreasing temperature, the pair correlation function in the plot gets more structured. This indicates that crystallization is happening.