Category:Electron-phonon interactions: Difference between revisions
No edit summary |
(Add workflow figure and add more details to text) |
||
| (11 intermediate revisions by 3 users not shown) | |||
| Line 9: | Line 9: | ||
== Theoretical background == | == Theoretical background == | ||
For a very comprehensive overview of the theory of electron-phonon coupling, we recommend reading | For a very comprehensive overview of the theory of electron-phonon coupling, we recommend reading reference {{cite|giustino:rmp:2017}}. | ||
The [[Electron-phonon interactions theory|stochastic approach]] allows obtaining the bandgap renormalization and an approximation of the electronic spectral function due to the ionic degrees of freedom under the static approximation using a supercell approach. This has the advantage that it can be easily implemented and used with different levels of theory to describe the electronic states, such as different exchange correlation functional or even the GW approximation. | The [[Electron-phonon interactions theory#Electron-phonon interactions from statistical sampling|stochastic approach]] allows obtaining the bandgap renormalization and an approximation of the electronic spectral function due to the ionic degrees of freedom under the static approximation using a supercell approach. This has the advantage that it can be easily implemented and used with different levels of theory to describe the electronic states, such as different exchange correlation functional or even the GW approximation. | ||
Another approach to include the coupling between the electronic and ionic degrees of freedom is by using the methods and language of many-body perturbation theory, where the coupling is included as a perturbation of the electronic or phononic states. | Another approach to include the coupling between the electronic and ionic degrees of freedom is by using the methods and language of many-body perturbation theory, where the coupling is included as a perturbation of the electronic or phononic states. | ||
In the case of the perturbation of the electronic states, we can access the bandgap renormalization as well as electronic transport coefficients with the inclusion of phonon scattering which is dominant in a wide range of applications such as mobility of semiconductors or conductivity of metals at room temperature. | In the case of the perturbation of the electronic states, we can access the bandgap renormalization as well as electronic transport coefficients with the inclusion of phonon scattering which is dominant in a wide range of applications such as mobility of semiconductors or conductivity of metals at room temperature. | ||
== | == Stochastic displacements approach == | ||
The stochastic approach implies the knowledge of the phonons on a supercell, these are then used to displace the atoms along a set of random or a single specially chosen direction | The stochastic approach implies the knowledge of the phonons on a supercell, these are then used to displace the atoms along a set of random or a single specially chosen direction {{cite|zacharias:prb:2016}} with the displacement length determined by the temperature of the ionic system. The bandgap can be directly obtained by averaging over the set of randomly displaced supercells, or from the aforementioned special displacement pattern. | ||
*[[Electron-phonon interactions from Monte-Carlo sampling]] | *[[Electron-phonon interactions from Monte-Carlo sampling]] | ||
== Perturbative approach == | |||
[[File:Elphon-workflow.png|400px|thumb|right|General workflow when running electron-phonon calculations using perturbation theory.]] | |||
The transport coefficients are computed within the framework of the linearized Boltzmann transport equation, which in turn requires the knowledge of the electronic lifetimes due to every possible scattering event. There are a few approximations for these scattering rates: in the constant-relaxation time approximation (CRTA), an empirical parameter is used to approximate the scattering rate throughout the Brillouin zone | When treating the electron-phonon interaction as a perturbation the central quantity that we need to compute becomes the electron-phonon matrix element which within the framework of DFT requires the knowledge of the change of Kohn-Sham potential with an ionic perturbation as well as the initial and final electronic Kohn-Sham states. This requires the calculation to be done in two steps. | ||
=== Electron-phonon potential from supercells === | |||
In the first step, we [[Electron-phonon_potential_from_supercells|obtain the derivatives of the Kohn-sham potential with respect to the ionic displacements]] | |||
::<math> | |||
\partial_{I \alpha} V (\mathbf{r}) = \frac{\partial V(r)}{\partial R_{I\alpha}} | |||
</math> | |||
with <math>I</math> the ion index and <math>\alpha</math> denoting the Cartesian direction in which it is displaced. | |||
These derivatives of the potential are stored in a {{FILE|phelel_params.hdf5}} file, which is required for computing the matrix elements in the next steps. | |||
=== Electron-phonon matrix elements and physical observables === | |||
Once we have the derivatives of the Kohn-Sham potential we can evaluate the electron-phonon matrix elements | |||
::<math> | |||
g_{mn \mathbf{k}, \nu \mathbf{q}} | |||
\equiv | |||
\langle | |||
\psi_{m \mathbf{k} - \mathbf{q}} | | |||
\partial_{\nu \mathbf{q}} V | | |||
\psi_{n \mathbf{k}} | |||
\rangle | |||
</math> | |||
which requires computing Kohn-Sham eigenstates <math>\psi_{n \mathbf{k}}</math> on a dense <b>k</b>-point mesh. | |||
This calculation is done in the primitive cell, where the potential derivative and related quantities are read from the previously generated {{FILE|phelel_params.hdf5}} file. | |||
==== [[Bandgap renormalization due to electron-phonon coupling]] ==== | |||
The bandgap renormalization is computed from the real part of the Fan-Migdal and Debye Waller contributions to the electron self-energy. | |||
To get an accurate value, we need to carefully consider both basis set (number of plane-waves and KS states) as well as <b>k</b>-points used to evaluate the electron self-energy. | |||
==== [[Transport coefficients including electron-phonon scattering]] ==== | |||
The transport coefficients are computed within the framework of the linearized Boltzmann transport equation, which in turn requires the knowledge of the electronic lifetimes due to every possible scattering event. There are a few approximations for these scattering rates: | |||
# in the constant-relaxation time approximation (CRTA), an empirical parameter is used to approximate the scattering rate <math>\tau_{n\mathbf{k}} = \tau</math> throughout the Brillouin zone | |||
# in the self-energy relaxation time approximation (SERTA) or energy relaxation time approximation (ERTA), the lifetimes are approximated from the electron self-energy <math>\tau_{n\mathbf{k}} = [2\Sigma_{n\mathbf{k}}(\epsilon_{n\mathbf{k}})]^{-1}</math> | |||
# in the momentum relaxation time approximation (MRTA) an additional geometric factor is included to account for the correct balance between inwards and outwards scattering. | |||
== References == | |||
<references/> | |||
Latest revision as of 14:41, 23 January 2025
In most of the features implemented in VASP, the electron and vibrational degrees of freedom (phonons) are treated separately. Electron-phonon coupling refers to the coupling of these two systems, and it can be used to include the effect of each system on the other while still treating the two systems separately.
The inclusion of the effects of the ionic degrees of freedom in the electronic structure is important in the determination of many physical observables such as the bandgap, spectral functions, electronic conductivity, Seebeck coefficient or electronic thermal conductivity to name a few.
With VASP, one can use different approaches to include these effects: by statistically averaging observables during a molecular dynamics calculation, by stochastically sampling the ionic degrees of freedom or using many-body perturbation theory. In this page we outline the two later approaches, their advantages and disadvantages and range of application.
Theoretical background
For a very comprehensive overview of the theory of electron-phonon coupling, we recommend reading reference [1].
The stochastic approach allows obtaining the bandgap renormalization and an approximation of the electronic spectral function due to the ionic degrees of freedom under the static approximation using a supercell approach. This has the advantage that it can be easily implemented and used with different levels of theory to describe the electronic states, such as different exchange correlation functional or even the GW approximation.
Another approach to include the coupling between the electronic and ionic degrees of freedom is by using the methods and language of many-body perturbation theory, where the coupling is included as a perturbation of the electronic or phononic states. In the case of the perturbation of the electronic states, we can access the bandgap renormalization as well as electronic transport coefficients with the inclusion of phonon scattering which is dominant in a wide range of applications such as mobility of semiconductors or conductivity of metals at room temperature.
Stochastic displacements approach
The stochastic approach implies the knowledge of the phonons on a supercell, these are then used to displace the atoms along a set of random or a single specially chosen direction [2] with the displacement length determined by the temperature of the ionic system. The bandgap can be directly obtained by averaging over the set of randomly displaced supercells, or from the aforementioned special displacement pattern.
Perturbative approach
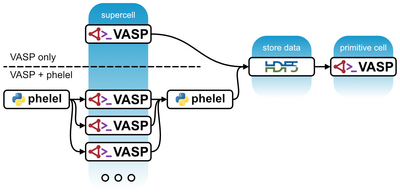
When treating the electron-phonon interaction as a perturbation the central quantity that we need to compute becomes the electron-phonon matrix element which within the framework of DFT requires the knowledge of the change of Kohn-Sham potential with an ionic perturbation as well as the initial and final electronic Kohn-Sham states. This requires the calculation to be done in two steps.
Electron-phonon potential from supercells
In the first step, we obtain the derivatives of the Kohn-sham potential with respect to the ionic displacements
with the ion index and denoting the Cartesian direction in which it is displaced. These derivatives of the potential are stored in a phelel_params.hdf5 file, which is required for computing the matrix elements in the next steps.
Electron-phonon matrix elements and physical observables
Once we have the derivatives of the Kohn-Sham potential we can evaluate the electron-phonon matrix elements
which requires computing Kohn-Sham eigenstates on a dense k-point mesh. This calculation is done in the primitive cell, where the potential derivative and related quantities are read from the previously generated phelel_params.hdf5 file.
Bandgap renormalization due to electron-phonon coupling
The bandgap renormalization is computed from the real part of the Fan-Migdal and Debye Waller contributions to the electron self-energy. To get an accurate value, we need to carefully consider both basis set (number of plane-waves and KS states) as well as k-points used to evaluate the electron self-energy.
Transport coefficients including electron-phonon scattering
The transport coefficients are computed within the framework of the linearized Boltzmann transport equation, which in turn requires the knowledge of the electronic lifetimes due to every possible scattering event. There are a few approximations for these scattering rates:
- in the constant-relaxation time approximation (CRTA), an empirical parameter is used to approximate the scattering rate throughout the Brillouin zone
- in the self-energy relaxation time approximation (SERTA) or energy relaxation time approximation (ERTA), the lifetimes are approximated from the electron self-energy
- in the momentum relaxation time approximation (MRTA) an additional geometric factor is included to account for the correct balance between inwards and outwards scattering.
References
Pages in category "Electron-phonon interactions"
The following 55 pages are in this category, out of 55 total.
E
- Electron-phonon interactions from Monte-Carlo sampling
- Electron-phonon interactions theory
- Electron-phonon potential from supercells
- ELPH DECOMPOSE
- ELPH DRIVER
- ELPH IGNORE IMAG PHONONS
- ELPH ISMEAR
- ELPH KSPACING
- ELPH LR
- ELPH MODE
- ELPH NBANDS
- ELPH NBANDS SUM
- ELPH POT FFT MESH
- ELPH POT GENERATE
- ELPH POT LATTICE
- ELPH PREPARE
- ELPH RUN
- ELPH SCATTERING APPROX
- ELPH SELFEN BAND START
- ELPH SELFEN BAND STOP
- ELPH SELFEN CARRIER DEN
- ELPH SELFEN CARRIER PER CELL
- ELPH SELFEN DELTA
- ELPH SELFEN DW
- ELPH SELFEN FAN
- ELPH SELFEN GAPS
- ELPH SELFEN IKPT
- ELPH SELFEN KPTS
- ELPH SELFEN MU
- ELPH SELFEN NW
- ELPH SELFEN STATIC
- ELPH SELFEN TEMPS
- ELPH SELFEN WRANGE
- ELPH TRANSPORT
- ELPH TRANSPORT DFERMI TOL
- ELPH TRANSPORT DRIVER
- ELPH TRANSPORT EMAX
- ELPH TRANSPORT EMIN
- ELPH USEBLAS
- ENCUTLR
